If there have been a set of survival guidelines for knowledge scientists, amongst them must be this: At all times report uncertainty estimates along with your predictions. Nevertheless, right here we’re, working with neural networks, and in contrast to lm, a Keras mannequin doesn’t conveniently output one thing like a commonplace error for the weights.
We would attempt to consider rolling your individual uncertainty measure – for instance, averaging predictions from networks skilled from completely different random weight initializations, for various numbers of epochs, or on completely different subsets of the info. However we would nonetheless be frightened that our technique is sort of a bit, nicely … advert hoc.
On this submit, we’ll see a each sensible in addition to theoretically grounded strategy to acquiring uncertainty estimates from neural networks. First, nevertheless, let’s shortly discuss why uncertainty is that essential – over and above its potential to save lots of an information scientist’s job.
Why uncertainty?
In a society the place automated algorithms are – and will likely be – entrusted with an increasing number of life-critical duties, one reply instantly jumps to thoughts: If the algorithm accurately quantifies its uncertainty, we could have human consultants examine the extra unsure predictions and doubtlessly revise them.
This can solely work if the community’s self-indicated uncertainty actually is indicative of a better likelihood of misclassification. Leibig et al.(Leibig et al. 2017) used a predecessor of the strategy described under to evaluate neural community uncertainty in detecting diabetic retinopathy. They discovered that certainly, the distributions of uncertainty had been completely different relying on whether or not the reply was appropriate or not:

Along with quantifying uncertainty, it might probably make sense to qualify it. Within the Bayesian deep studying literature, a distinction is usually made between epistemic uncertainty and aleatoric uncertainty (Kendall and Gal 2017).
Epistemic uncertainty refers to imperfections within the mannequin – within the restrict of infinite knowledge, this type of uncertainty needs to be reducible to 0. Aleatoric uncertainty is because of knowledge sampling and measurement processes and doesn’t rely on the dimensions of the dataset.
Say we practice a mannequin for object detection. With extra knowledge, the mannequin ought to change into extra positive about what makes a unicycle completely different from a mountainbike. Nevertheless, let’s assume all that’s seen of the mountainbike is the entrance wheel, the fork and the top tube. Then it doesn’t look so completely different from a unicycle any extra!
What could be the results if we may distinguish each varieties of uncertainty? If epistemic uncertainty is excessive, we are able to attempt to get extra coaching knowledge. The remaining aleatoric uncertainty ought to then preserve us cautioned to consider security margins in our utility.
In all probability no additional justifications are required of why we would need to assess mannequin uncertainty – however how can we do that?
Uncertainty estimates by means of Bayesian deep studying
In a Bayesian world, in precept, uncertainty is free of charge as we don’t simply get level estimates (the utmost aposteriori) however the full posterior distribution. Strictly talking, in Bayesian deep studying, priors needs to be put over the weights, and the posterior be decided in keeping with Bayes’ rule.
To the deep studying practitioner, this sounds fairly arduous – and the way do you do it utilizing Keras?
In 2016 although, Gal and Ghahramani (Yarin Gal and Ghahramani 2016) confirmed that when viewing a neural community as an approximation to a Gaussian course of, uncertainty estimates might be obtained in a theoretically grounded but very sensible approach: by coaching a community with dropout after which, utilizing dropout at check time too. At check time, dropout lets us extract Monte Carlo samples from the posterior, which may then be used to approximate the true posterior distribution.
That is already excellent news, however it leaves one query open: How can we select an acceptable dropout fee? The reply is: let the community be taught it.
Studying dropout and uncertainty
In a number of 2017 papers (Y. Gal, Hron, and Kendall 2017),(Kendall and Gal 2017), Gal and his coworkers demonstrated how a community might be skilled to dynamically adapt the dropout fee so it’s enough for the quantity and traits of the info given.
In addition to the predictive imply of the goal variable, it might probably moreover be made to be taught the variance.
This implies we are able to calculate each varieties of uncertainty, epistemic and aleatoric, independently, which is helpful within the gentle of their completely different implications. We then add them as much as acquire the general predictive uncertainty.
Let’s make this concrete and see how we are able to implement and check the supposed habits on simulated knowledge.
Within the implementation, there are three issues warranting our particular consideration:
- The wrapper class used so as to add learnable-dropout habits to a Keras layer;
- The loss perform designed to attenuate aleatoric uncertainty; and
- The methods we are able to acquire each uncertainties at check time.
Let’s begin with the wrapper.
A wrapper for studying dropout
On this instance, we’ll limit ourselves to studying dropout for dense layers. Technically, we’ll add a weight and a loss to each dense layer we need to use dropout with. This implies we’ll create a customized wrapper class that has entry to the underlying layer and may modify it.
The logic carried out within the wrapper is derived mathematically within the Concrete Dropout paper (Y. Gal, Hron, and Kendall 2017). The under code is a port to R of the Python Keras model discovered within the paper’s companion github repo.
So first, right here is the wrapper class – we’ll see find out how to use it in only a second:
library(keras)
# R6 wrapper class, a subclass of KerasWrapper
ConcreteDropout <- R6::R6Class("ConcreteDropout",
inherit = KerasWrapper,
public = record(
weight_regularizer = NULL,
dropout_regularizer = NULL,
init_min = NULL,
init_max = NULL,
is_mc_dropout = NULL,
supports_masking = TRUE,
p_logit = NULL,
p = NULL,
initialize = perform(weight_regularizer,
dropout_regularizer,
init_min,
init_max,
is_mc_dropout) {
self$weight_regularizer <- weight_regularizer
self$dropout_regularizer <- dropout_regularizer
self$is_mc_dropout <- is_mc_dropout
self$init_min <- k_log(init_min) - k_log(1 - init_min)
self$init_max <- k_log(init_max) - k_log(1 - init_max)
},
construct = perform(input_shape) {
tremendous$construct(input_shape)
self$p_logit <- tremendous$add_weight(
identify = "p_logit",
form = form(1),
initializer = initializer_random_uniform(self$init_min, self$init_max),
trainable = TRUE
)
self$p <- k_sigmoid(self$p_logit)
input_dim <- input_shape[[2]]
weight <- personal$py_wrapper$layer$kernel
kernel_regularizer <- self$weight_regularizer *
k_sum(k_square(weight)) /
(1 - self$p)
dropout_regularizer <- self$p * k_log(self$p)
dropout_regularizer <- dropout_regularizer +
(1 - self$p) * k_log(1 - self$p)
dropout_regularizer <- dropout_regularizer *
self$dropout_regularizer *
k_cast(input_dim, k_floatx())
regularizer <- k_sum(kernel_regularizer + dropout_regularizer)
tremendous$add_loss(regularizer)
},
concrete_dropout = perform(x) {
eps <- k_cast_to_floatx(k_epsilon())
temp <- 0.1
unif_noise <- k_random_uniform(form = k_shape(x))
drop_prob <- k_log(self$p + eps) -
k_log(1 - self$p + eps) +
k_log(unif_noise + eps) -
k_log(1 - unif_noise + eps)
drop_prob <- k_sigmoid(drop_prob / temp)
random_tensor <- 1 - drop_prob
retain_prob <- 1 - self$p
x <- x * random_tensor
x <- x / retain_prob
x
},
name = perform(x, masks = NULL, coaching = NULL) {
if (self$is_mc_dropout) {
tremendous$name(self$concrete_dropout(x))
} else {
k_in_train_phase(
perform()
tremendous$name(self$concrete_dropout(x)),
tremendous$name(x),
coaching = coaching
)
}
}
)
)
# perform for instantiating customized wrapper
layer_concrete_dropout <- perform(object,
layer,
weight_regularizer = 1e-6,
dropout_regularizer = 1e-5,
init_min = 0.1,
init_max = 0.1,
is_mc_dropout = TRUE,
identify = NULL,
trainable = TRUE) {
create_wrapper(ConcreteDropout, object, record(
layer = layer,
weight_regularizer = weight_regularizer,
dropout_regularizer = dropout_regularizer,
init_min = init_min,
init_max = init_max,
is_mc_dropout = is_mc_dropout,
identify = identify,
trainable = trainable
))
}The wrapper instantiator has default arguments, however two of them needs to be tailored to the info: weight_regularizer and dropout_regularizer. Following the authors’ suggestions, they need to be set as follows.
First, select a price for hyperparameter (l). On this view of a neural community as an approximation to a Gaussian course of, (l) is the prior length-scale, our a priori assumption concerning the frequency traits of the info. Right here, we observe Gal’s demo in setting l := 1e-4. Then the preliminary values for weight_regularizer and dropout_regularizer are derived from the length-scale and the pattern measurement.
# pattern measurement (coaching knowledge)
n_train <- 1000
# pattern measurement (validation knowledge)
n_val <- 1000
# prior length-scale
l <- 1e-4
# preliminary worth for weight regularizer
wd <- l^2/n_train
# preliminary worth for dropout regularizer
dd <- 2/n_trainNow let’s see find out how to use the wrapper in a mannequin.
Dropout mannequin
In our demonstration, we’ll have a mannequin with three hidden dense layers, every of which can have its dropout fee calculated by a devoted wrapper.
# we use one-dimensional enter knowledge right here, however this is not a necessity
input_dim <- 1
# this too may very well be > 1 if we needed
output_dim <- 1
hidden_dim <- 1024
enter <- layer_input(form = input_dim)
output <- enter %>% layer_concrete_dropout(
layer = layer_dense(items = hidden_dim, activation = "relu"),
weight_regularizer = wd,
dropout_regularizer = dd
) %>% layer_concrete_dropout(
layer = layer_dense(items = hidden_dim, activation = "relu"),
weight_regularizer = wd,
dropout_regularizer = dd
) %>% layer_concrete_dropout(
layer = layer_dense(items = hidden_dim, activation = "relu"),
weight_regularizer = wd,
dropout_regularizer = dd
)Now, mannequin output is fascinating: We have now the mannequin yielding not simply the predictive (conditional) imply, but additionally the predictive variance ((tau^{-1}) in Gaussian course of parlance):
imply <- output %>% layer_concrete_dropout(
layer = layer_dense(items = output_dim),
weight_regularizer = wd,
dropout_regularizer = dd
)
log_var <- output %>% layer_concrete_dropout(
layer_dense(items = output_dim),
weight_regularizer = wd,
dropout_regularizer = dd
)
output <- layer_concatenate(record(imply, log_var))
mannequin <- keras_model(enter, output)The numerous factor right here is that we be taught completely different variances for various knowledge factors. We thus hope to have the ability to account for heteroscedasticity (completely different levels of variability) within the knowledge.
Heteroscedastic loss
Accordingly, as an alternative of imply squared error we use a value perform that doesn’t deal with all estimates alike(Kendall and Gal 2017):
[frac{1}{N} sum_i{frac{1}{2 hat{sigma}^2_i} (mathbf{y}_i – mathbf{hat{y}}_i)^2 + frac{1}{2} log hat{sigma}^2_i}]
Along with the compulsory goal vs. prediction examine, this price perform comprises two regularization phrases:
- First, (frac{1}{2 hat{sigma}^2_i}) downweights the high-uncertainty predictions within the loss perform. Put plainly: The mannequin is inspired to point excessive uncertainty when its predictions are false.
- Second, (frac{1}{2} log hat{sigma}^2_i) makes positive the community doesn’t merely point out excessive uncertainty in every single place.
This logic maps on to the code (besides that as typical, we’re calculating with the log of the variance, for causes of numerical stability):
heteroscedastic_loss <- perform(y_true, y_pred) {
imply <- y_pred[, 1:output_dim]
log_var <- y_pred[, (output_dim + 1):(output_dim * 2)]
precision <- k_exp(-log_var)
k_sum(precision * (y_true - imply) ^ 2 + log_var, axis = 2)
}Coaching on simulated knowledge
Now we generate some check knowledge and practice the mannequin.
gen_data_1d <- perform(n) {
sigma <- 1
X <- matrix(rnorm(n))
w <- 2
b <- 8
Y <- matrix(X %*% w + b + sigma * rnorm(n))
record(X, Y)
}
c(X, Y) %<-% gen_data_1d(n_train + n_val)
c(X_train, Y_train) %<-% record(X[1:n_train], Y[1:n_train])
c(X_val, Y_val) %<-% record(X[(n_train + 1):(n_train + n_val)],
Y[(n_train + 1):(n_train + n_val)])
mannequin %>% compile(
optimizer = "adam",
loss = heteroscedastic_loss,
metrics = c(custom_metric("heteroscedastic_loss", heteroscedastic_loss))
)
historical past <- mannequin %>% match(
X_train,
Y_train,
epochs = 30,
batch_size = 10
)With coaching completed, we flip to the validation set to acquire estimates on unseen knowledge – together with these uncertainty measures that is all about!
Get hold of uncertainty estimates by way of Monte Carlo sampling
As usually in a Bayesian setup, we assemble the posterior (and thus, the posterior predictive) by way of Monte Carlo sampling.
Not like in conventional use of dropout, there isn’t any change in habits between coaching and check phases: Dropout stays “on.”
So now we get an ensemble of mannequin predictions on the validation set:
Bear in mind, our mannequin predicts the imply in addition to the variance. We’ll use the previous for calculating epistemic uncertainty, whereas aleatoric uncertainty is obtained from the latter.
First, we decide the predictive imply as a mean of the MC samples’ imply output:
# the means are within the first output column
means <- MC_samples[, , 1:output_dim]
# common over the MC samples
predictive_mean <- apply(means, 2, imply) To calculate epistemic uncertainty, we once more use the imply output, however this time we’re within the variance of the MC samples:
epistemic_uncertainty <- apply(means, 2, var) Then aleatoric uncertainty is the typical over the MC samples of the variance output..
Word how this process provides us uncertainty estimates individually for each prediction. How do they give the impression of being?
df <- knowledge.body(
x = X_val,
y_pred = predictive_mean,
e_u_lower = predictive_mean - sqrt(epistemic_uncertainty),
e_u_upper = predictive_mean + sqrt(epistemic_uncertainty),
a_u_lower = predictive_mean - sqrt(aleatoric_uncertainty),
a_u_upper = predictive_mean + sqrt(aleatoric_uncertainty),
u_overall_lower = predictive_mean -
sqrt(epistemic_uncertainty) -
sqrt(aleatoric_uncertainty),
u_overall_upper = predictive_mean +
sqrt(epistemic_uncertainty) +
sqrt(aleatoric_uncertainty)
)Right here, first, is epistemic uncertainty, with shaded bands indicating one commonplace deviation above resp. under the anticipated imply:
ggplot(df, aes(x, y_pred)) +
geom_point() +
geom_ribbon(aes(ymin = e_u_lower, ymax = e_u_upper), alpha = 0.3)
That is fascinating. The coaching knowledge (in addition to the validation knowledge) had been generated from a typical regular distribution, so the mannequin has encountered many extra examples near the imply than exterior two, and even three, commonplace deviations. So it accurately tells us that in these extra unique areas, it feels fairly uncertain about its predictions.
That is precisely the habits we would like: Danger in robotically making use of machine studying strategies arises because of unanticipated variations between the coaching and check (actual world) distributions. If the mannequin had been to inform us “ehm, probably not seen something like that earlier than, don’t actually know what to do” that’d be an enormously priceless end result.
So whereas epistemic uncertainty has the algorithm reflecting on its mannequin of the world – doubtlessly admitting its shortcomings – aleatoric uncertainty, by definition, is irreducible. In fact, that doesn’t make it any much less priceless – we’d know we all the time need to consider a security margin. So how does it look right here?

Certainly, the extent of uncertainty doesn’t rely on the quantity of knowledge seen at coaching time.
Lastly, we add up each varieties to acquire the general uncertainty when making predictions.

Now let’s do this technique on a real-world dataset.
Mixed cycle energy plant electrical vitality output estimation
This dataset is out there from the UCI Machine Studying Repository. We explicitly selected a regression process with steady variables completely, to make for a easy transition from the simulated knowledge.
Within the dataset suppliers’ personal phrases
The dataset comprises 9568 knowledge factors collected from a Mixed Cycle Energy Plant over 6 years (2006-2011), when the ability plant was set to work with full load. Options encompass hourly common ambient variables Temperature (T), Ambient Strain (AP), Relative Humidity (RH) and Exhaust Vacuum (V) to foretell the online hourly electrical vitality output (EP) of the plant.
A mixed cycle energy plant (CCPP) consists of gasoline generators (GT), steam generators (ST) and warmth restoration steam mills. In a CCPP, the electrical energy is generated by gasoline and steam generators, that are mixed in a single cycle, and is transferred from one turbine to a different. Whereas the Vacuum is collected from and has impact on the Steam Turbine, the opposite three of the ambient variables impact the GT efficiency.
We thus have 4 predictors and one goal variable. We’ll practice 5 fashions: 4 single-variable regressions and one making use of all 4 predictors. It in all probability goes with out saying that our aim right here is to examine uncertainty info, to not fine-tune the mannequin.
Setup
Let’s shortly examine these 5 variables. Right here PE is vitality output, the goal variable.

We scale and divide up the info
and prepare for coaching just a few fashions.
n <- nrow(X_train)
n_epochs <- 100
batch_size <- 100
output_dim <- 1
num_MC_samples <- 20
l <- 1e-4
wd <- l^2/n
dd <- 2/n
get_model <- perform(input_dim, hidden_dim) {
enter <- layer_input(form = input_dim)
output <-
enter %>% layer_concrete_dropout(
layer = layer_dense(items = hidden_dim, activation = "relu"),
weight_regularizer = wd,
dropout_regularizer = dd
) %>% layer_concrete_dropout(
layer = layer_dense(items = hidden_dim, activation = "relu"),
weight_regularizer = wd,
dropout_regularizer = dd
) %>% layer_concrete_dropout(
layer = layer_dense(items = hidden_dim, activation = "relu"),
weight_regularizer = wd,
dropout_regularizer = dd
)
imply <-
output %>% layer_concrete_dropout(
layer = layer_dense(items = output_dim),
weight_regularizer = wd,
dropout_regularizer = dd
)
log_var <-
output %>% layer_concrete_dropout(
layer_dense(items = output_dim),
weight_regularizer = wd,
dropout_regularizer = dd
)
output <- layer_concatenate(record(imply, log_var))
mannequin <- keras_model(enter, output)
heteroscedastic_loss <- perform(y_true, y_pred) {
imply <- y_pred[, 1:output_dim]
log_var <- y_pred[, (output_dim + 1):(output_dim * 2)]
precision <- k_exp(-log_var)
k_sum(precision * (y_true - imply) ^ 2 + log_var, axis = 2)
}
mannequin %>% compile(optimizer = "adam",
loss = heteroscedastic_loss,
metrics = c("mse"))
mannequin
}We’ll practice every of the 5 fashions with a hidden_dim of 64.
We then acquire 20 Monte Carlo pattern from the posterior predictive distribution and calculate the uncertainties as earlier than.
Right here we present the code for the primary predictor, “AT.” It’s comparable for all different instances.
mannequin <- get_model(1, 64)
hist <- mannequin %>% match(
X_train[ ,1],
y_train,
validation_data = record(X_val[ , 1], y_val),
epochs = n_epochs,
batch_size = batch_size
)
MC_samples <- array(0, dim = c(num_MC_samples, nrow(X_val), 2 * output_dim))
for (okay in 1:num_MC_samples) {
MC_samples[k, ,] <- (mannequin %>% predict(X_val[ ,1]))
}
means <- MC_samples[, , 1:output_dim]
predictive_mean <- apply(means, 2, imply)
epistemic_uncertainty <- apply(means, 2, var)
logvar <- MC_samples[, , (output_dim + 1):(output_dim * 2)]
aleatoric_uncertainty <- exp(colMeans(logvar))
preds <- knowledge.body(
x1 = X_val[, 1],
y_true = y_val,
y_pred = predictive_mean,
e_u_lower = predictive_mean - sqrt(epistemic_uncertainty),
e_u_upper = predictive_mean + sqrt(epistemic_uncertainty),
a_u_lower = predictive_mean - sqrt(aleatoric_uncertainty),
a_u_upper = predictive_mean + sqrt(aleatoric_uncertainty),
u_overall_lower = predictive_mean -
sqrt(epistemic_uncertainty) -
sqrt(aleatoric_uncertainty),
u_overall_upper = predictive_mean +
sqrt(epistemic_uncertainty) +
sqrt(aleatoric_uncertainty)
)End result
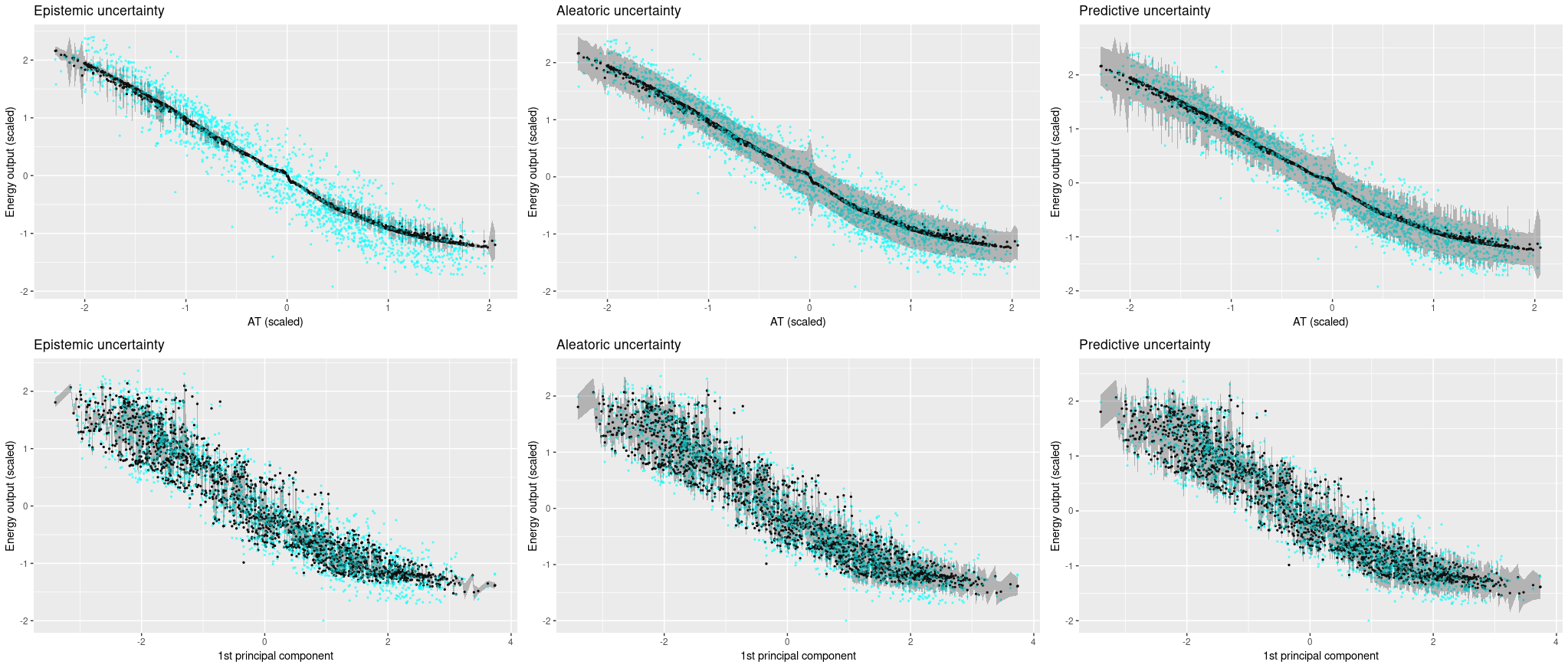
Now let’s see the uncertainty estimates for all 5 fashions!
First, the single-predictor setup. Floor reality values are displayed in cyan, posterior predictive estimates are black, and the gray bands prolong up resp. down by the sq. root of the calculated uncertainties.
We’re beginning with ambient temperature, a low-variance predictor.
We’re stunned how assured the mannequin is that it’s gotten the method logic appropriate, however excessive aleatoric uncertainty makes up for this (kind of).

Now trying on the different predictors, the place variance is far increased within the floor reality, it does get a bit troublesome to really feel snug with the mannequin’s confidence. Aleatoric uncertainty is excessive, however not excessive sufficient to seize the true variability within the knowledge. And we certaintly would hope for increased epistemic uncertainty, particularly in locations the place the mannequin introduces arbitrary-looking deviations from linearity.



Now let’s see uncertainty output after we use all 4 predictors. We see that now, the Monte Carlo estimates range much more, and accordingly, epistemic uncertainty is so much increased. Aleatoric uncertainty, alternatively, received so much decrease. Total, predictive uncertainty captures the vary of floor reality values fairly nicely.

Conclusion
We’ve launched a way to acquire theoretically grounded uncertainty estimates from neural networks.
We discover the strategy intuitively engaging for a number of causes: For one, the separation of various kinds of uncertainty is convincing and virtually related. Second, uncertainty depends upon the quantity of knowledge seen within the respective ranges. That is particularly related when considering of variations between coaching and test-time distributions.
Third, the thought of getting the community “change into conscious of its personal uncertainty” is seductive.
In apply although, there are open questions as to find out how to apply the strategy. From our real-world check above, we instantly ask: Why is the mannequin so assured when the bottom reality knowledge has excessive variance? And, considering experimentally: How would that adjust with completely different knowledge sizes (rows), dimensionality (columns), and hyperparameter settings (together with neural community hyperparameters like capability, variety of epochs skilled, and activation features, but additionally the Gaussian course of prior length-scale (tau))?
For sensible use, extra experimentation with completely different datasets and hyperparameter settings is actually warranted.
One other path to observe up is utility to duties in picture recognition, akin to semantic segmentation.
Right here we’d be concerned with not simply quantifying, but additionally localizing uncertainty, to see which visible elements of a scene (occlusion, illumination, unusual shapes) make objects onerous to establish.