In cooperative multi-agent reinforcement studying (MARL), because of its on-policy nature, coverage gradient (PG) strategies are usually believed to be much less pattern environment friendly than worth decomposition (VD) strategies, that are off-policy. Nevertheless, some current empirical research exhibit that with correct enter illustration and hyper-parameter tuning, multi-agent PG can obtain surprisingly sturdy efficiency in comparison with off-policy VD strategies.
Why may PG strategies work so properly? On this publish, we are going to current concrete evaluation to indicate that in sure situations, e.g., environments with a extremely multi-modal reward panorama, VD may be problematic and result in undesired outcomes. Against this, PG strategies with particular person insurance policies can converge to an optimum coverage in these circumstances. As well as, PG strategies with auto-regressive (AR) insurance policies can be taught multi-modal insurance policies.
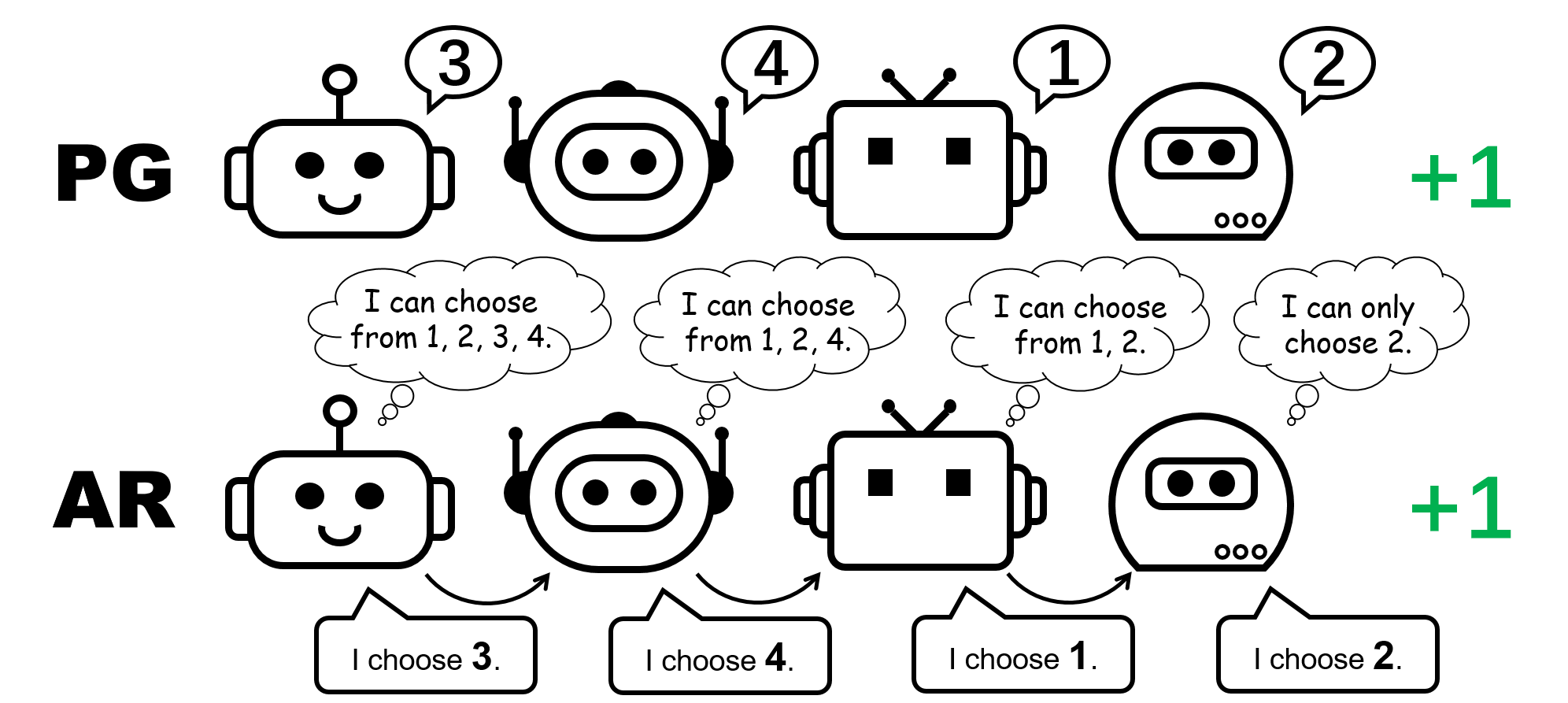
Determine 1: completely different coverage illustration for the 4-player permutation recreation.
CTDE in Cooperative MARL: VD and PG strategies
Centralized coaching and decentralized execution (CTDE) is a well-liked framework in cooperative MARL. It leverages international data for more practical coaching whereas preserving the illustration of particular person insurance policies for testing. CTDE may be applied by way of worth decomposition (VD) or coverage gradient (PG), main to 2 several types of algorithms.
VD strategies be taught native Q networks and a mixing operate that mixes the native Q networks to a world Q operate. The blending operate is often enforced to fulfill the Particular person-World-Max (IGM) precept, which ensures the optimum joint motion may be computed by greedily selecting the optimum motion domestically for every agent.
Against this, PG strategies straight apply coverage gradient to be taught a person coverage and a centralized worth operate for every agent. The worth operate takes as its enter the worldwide state (e.g., MAPPO) or the concatenation of all of the native observations (e.g., MADDPG), for an correct international worth estimate.
The permutation recreation: a easy counterexample the place VD fails
We begin our evaluation by contemplating a stateless cooperative recreation, specifically the permutation recreation. In an $N$-player permutation recreation, every agent can output $N$ actions ${ 1,ldots, N }$. Brokers obtain $+1$ reward if their actions are mutually completely different, i.e., the joint motion is a permutation over $1, ldots, N$; in any other case, they obtain $0$ reward. Notice that there are $N!$ symmetric optimum methods on this recreation.
Determine 2: the 4-player permutation recreation.
Allow us to give attention to the 2-player permutation recreation for our dialogue. On this setting, if we apply VD to the sport, the worldwide Q-value will factorize to
[Q_textrm{tot}(a^1,a^2)=f_textrm{mix}(Q_1(a^1),Q_2(a^2)),]
the place $Q_1$ and $Q_2$ are native Q-functions, $Q_textrm{tot}$ is the worldwide Q-function, and $f_textrm{combine}$ is the blending operate that, as required by VD strategies, satisfies the IGM precept.
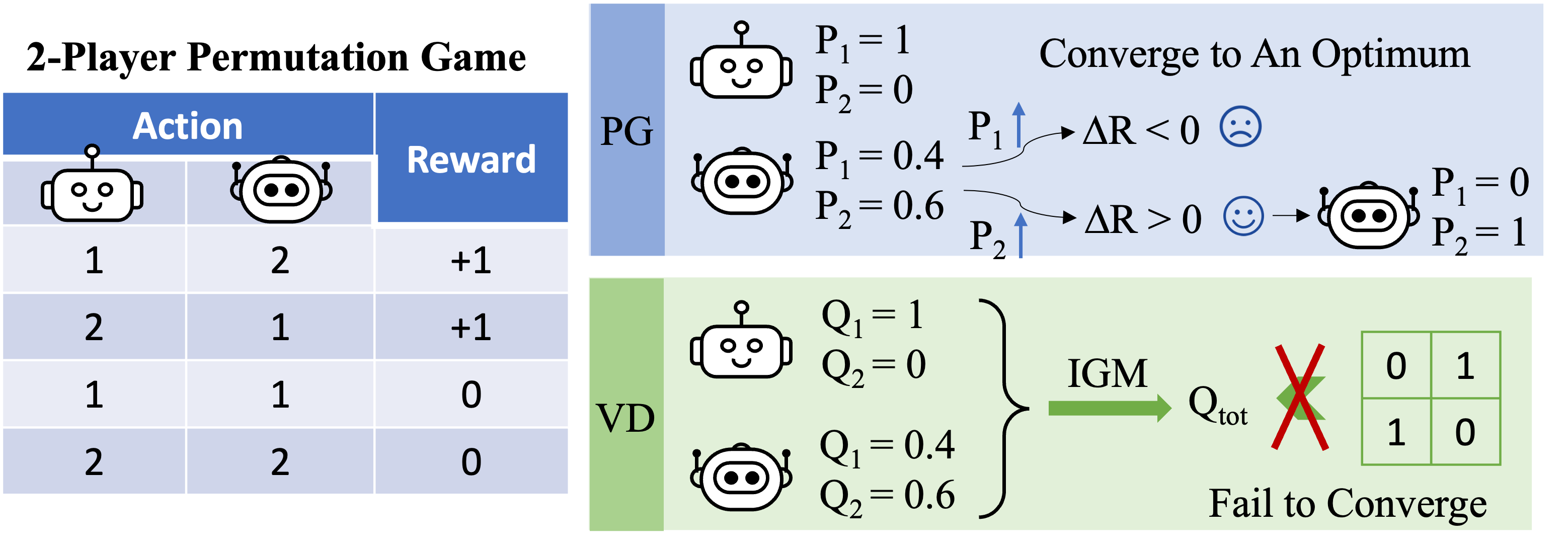
Determine 3: high-level instinct on why VD fails within the 2-player permutation recreation.
We formally show that VD can not characterize the payoff of the 2-player permutation recreation by contradiction. If VD strategies have been in a position to characterize the payoff, we might have
[Q_textrm{tot}(1, 2)=Q_textrm{tot}(2,1)=1 qquad textrm{and} qquad Q_textrm{tot}(1, 1)=Q_textrm{tot}(2,2)=0.]
Nevertheless, if both of those two brokers have completely different native Q values, e.g. $Q_1(1)> Q_1(2)$, then in accordance with the IGM precept, we should have
[1=Q_textrm{tot}(1,2)=argmax_{a^2}Q_textrm{tot}(1,a^2)>argmax_{a^2}Q_textrm{tot}(2,a^2)=Q_textrm{tot}(2,1)=1.]
In any other case, if $Q_1(1)=Q_1(2)$ and $Q_2(1)=Q_2(2)$, then
[Q_textrm{tot}(1, 1)=Q_textrm{tot}(2,2)=Q_textrm{tot}(1, 2)=Q_textrm{tot}(2,1).]
Because of this, worth decomposition can not characterize the payoff matrix of the 2-player permutation recreation.
What about PG strategies? Particular person insurance policies can certainly characterize an optimum coverage for the permutation recreation. Furthermore, stochastic gradient descent can assure PG to converge to certainly one of these optima underneath delicate assumptions. This means that, though PG strategies are much less widespread in MARL in contrast with VD strategies, they are often preferable in sure circumstances which are frequent in real-world purposes, e.g., video games with a number of technique modalities.
We additionally comment that within the permutation recreation, to be able to characterize an optimum joint coverage, every agent should select distinct actions. Consequently, a profitable implementation of PG should be certain that the insurance policies are agent-specific. This may be completed through the use of both particular person insurance policies with unshared parameters (known as PG-Ind in our paper), or an agent-ID conditioned coverage (PG-ID).
PG outperform finest VD strategies on widespread MARL testbeds
Going past the straightforward illustrative instance of the permutation recreation, we prolong our research to widespread and extra real looking MARL benchmarks. Along with StarCraft Multi-Agent Problem (SMAC), the place the effectiveness of PG and agent-conditioned coverage enter has been verified, we present new ends in Google Analysis Soccer (GRF) and multi-player Hanabi Problem.
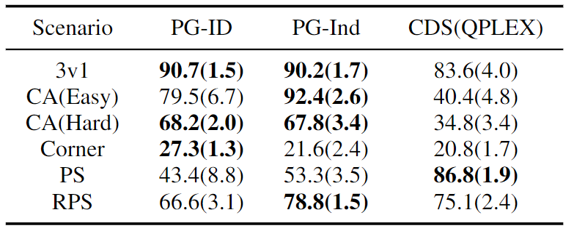
Determine 4: (left) profitable charges of PG strategies on GRF; (proper) finest and common analysis scores on Hanabi-Full.
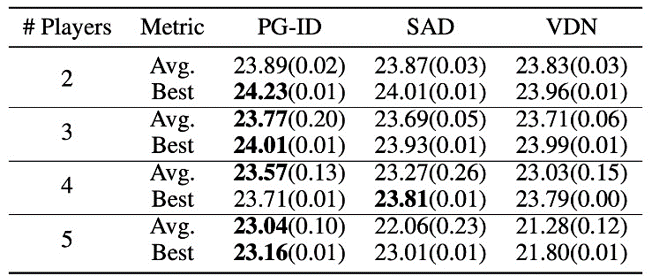
In GRF, PG strategies outperform the state-of-the-art VD baseline (CDS) in 5 situations. Apparently, we additionally discover that particular person insurance policies (PG-Ind) with out parameter sharing obtain comparable, generally even greater profitable charges, in comparison with agent-specific insurance policies (PG-ID) in all 5 situations. We consider PG-ID within the full-scale Hanabi recreation with various numbers of gamers (2-5 gamers) and examine them to SAD, a robust off-policy Q-learning variant in Hanabi, and Worth Decomposition Networks (VDN). As demonstrated within the above desk, PG-ID is ready to produce outcomes corresponding to or higher than one of the best and common rewards achieved by SAD and VDN with various numbers of gamers utilizing the identical variety of atmosphere steps.
Past greater rewards: studying multi-modal conduct by way of auto-regressive coverage modeling
Moreover studying greater rewards, we additionally research learn how to be taught multi-modal insurance policies in cooperative MARL. Let’s return to the permutation recreation. Though we’ve got proved that PG can successfully be taught an optimum coverage, the technique mode that it lastly reaches can extremely rely upon the coverage initialization. Thus, a pure query might be:
Can we be taught a single coverage that may cowl all of the optimum modes?
Within the decentralized PG formulation, the factorized illustration of a joint coverage can solely characterize one explicit mode. Subsequently, we suggest an enhanced approach to parameterize the insurance policies for stronger expressiveness — the auto-regressive (AR) insurance policies.

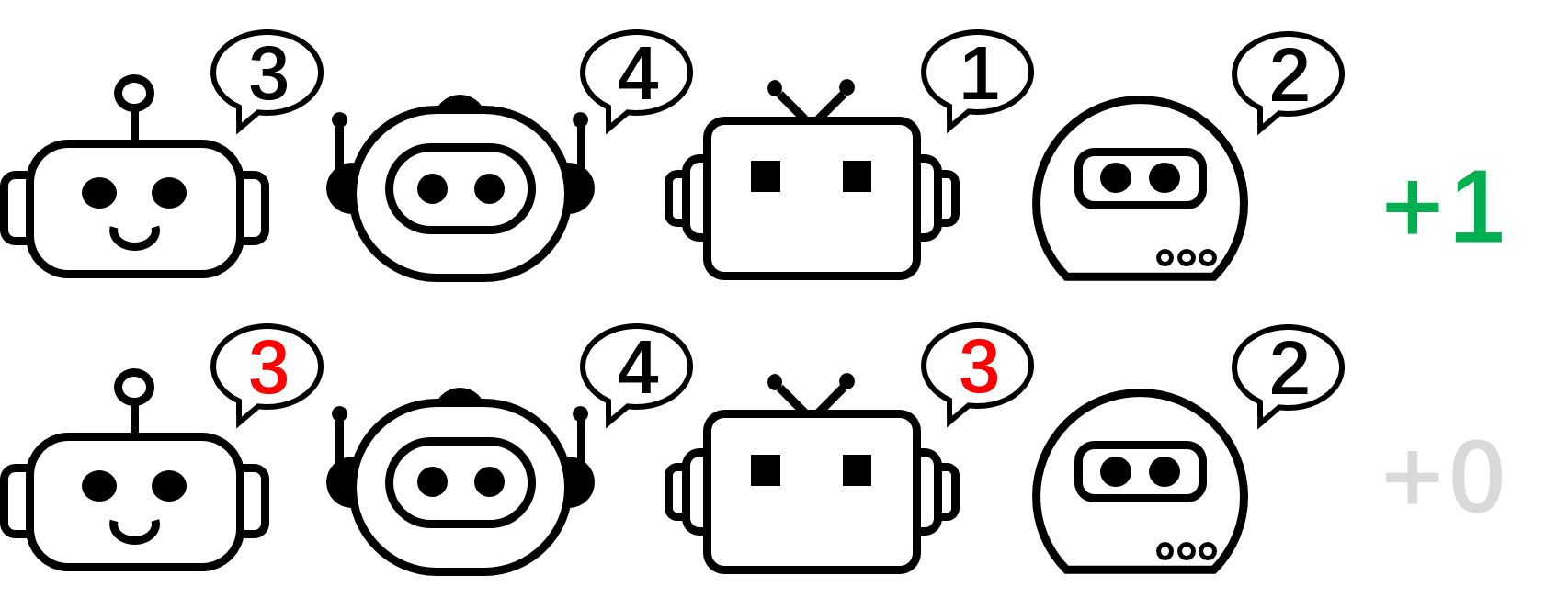
Determine 5: comparability between particular person insurance policies (PG) and auto-regressive insurance policies (AR) within the 4-player permutation recreation.
Formally, we factorize the joint coverage of $n$ brokers into the type of
[pi(mathbf{a} mid mathbf{o}) approx prod_{i=1}^n pi_{theta^{i}} left( a^{i}mid o^{i},a^{1},ldots,a^{i-1} right),]
the place the motion produced by agent $i$ relies upon by itself statement $o_i$ and all of the actions from earlier brokers $1,dots,i-1$. The auto-regressive factorization can characterize any joint coverage in a centralized MDP. The solely modification to every agent’s coverage is the enter dimension, which is barely enlarged by together with earlier actions; and the output dimension of every agent’s coverage stays unchanged.
With such a minimal parameterization overhead, AR coverage considerably improves the illustration energy of PG strategies. We comment that PG with AR coverage (PG-AR) can concurrently characterize all optimum coverage modes within the permutation recreation.

Determine: the heatmaps of actions for insurance policies discovered by PG-Ind (left) and PG-AR (center), and the heatmap for rewards (proper); whereas PG-Ind solely converge to a particular mode within the 4-player permutation recreation, PG-AR efficiently discovers all of the optimum modes.
In additional complicated environments, together with SMAC and GRF, PG-AR can be taught attention-grabbing emergent behaviors that require sturdy intra-agent coordination which will by no means be discovered by PG-Ind.
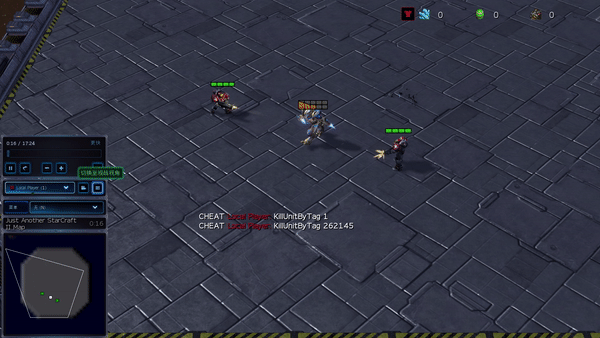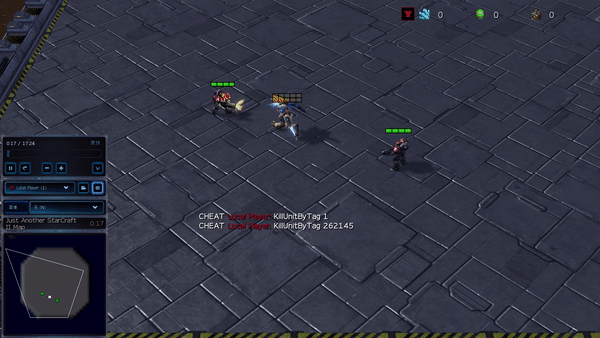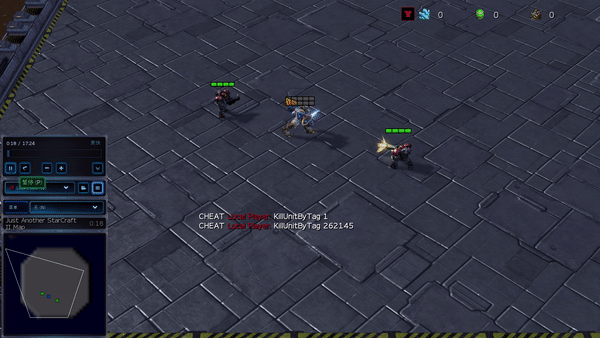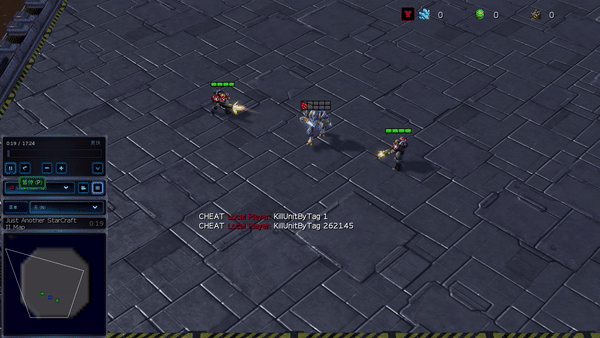
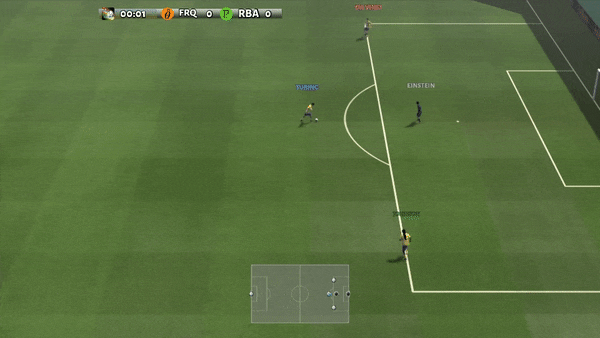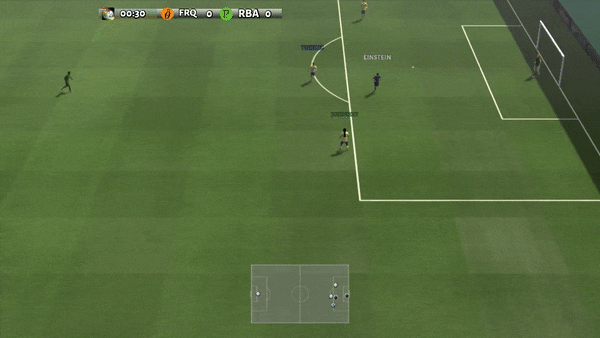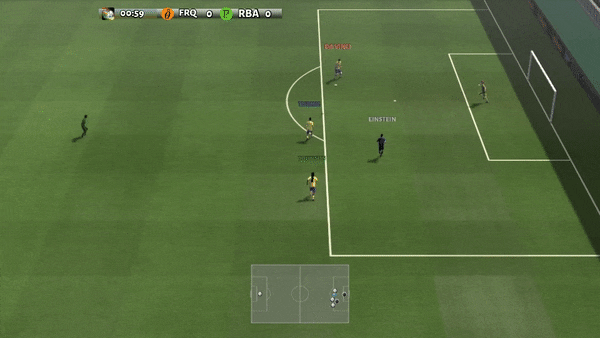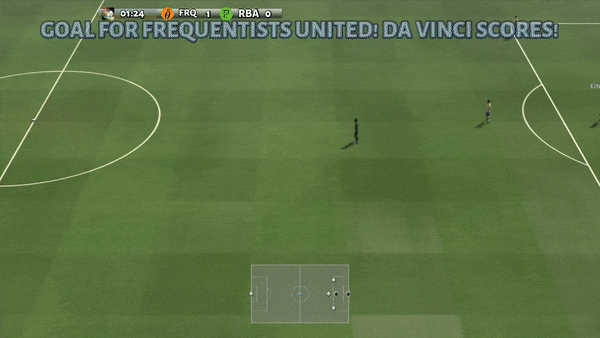
Determine 6: (left) emergent conduct induced by PG-AR in SMAC and GRF. On the 2m_vs_1z map of SMAC, the marines preserve standing and assault alternately whereas guaranteeing there is just one attacking marine at every timestep; (proper) within the academy_3_vs_1_with_keeper situation of GRF, brokers be taught a “Tiki-Taka” model conduct: every participant retains passing the ball to their teammates.
Discussions and Takeaways
On this publish, we offer a concrete evaluation of VD and PG strategies in cooperative MARL. First, we reveal the limitation on the expressiveness of widespread VD strategies, displaying that they might not characterize optimum insurance policies even in a easy permutation recreation. Against this, we present that PG strategies are provably extra expressive. We empirically confirm the expressiveness benefit of PG on widespread MARL testbeds, together with SMAC, GRF, and Hanabi Problem. We hope the insights from this work may gain advantage the neighborhood in direction of extra basic and extra highly effective cooperative MARL algorithms sooner or later.
This publish is predicated on our paper in joint with Zelai Xu: Revisiting Some Frequent Practices in Cooperative Multi-Agent Reinforcement Studying (paper, web site).