Time Sequence Forecasting with Recurrent Neural Networks

Overview

On this publish, we’ll evaluation three superior methods for enhancing the efficiency and generalization energy of recurrent neural networks. By the top of the part, you’ll know most of what there may be to learn about utilizing recurrent networks with Keras. We’ll display all three ideas on a temperature-forecasting drawback, the place you could have entry to a time collection of knowledge factors coming from sensors put in on the roof of a constructing, akin to temperature, air stress, and humidity, which you utilize to foretell what the temperature shall be 24 hours after the final knowledge level. It is a pretty difficult drawback that exemplifies many widespread difficulties encountered when working with time collection.

We’ll cowl the next methods:

• Recurrent dropout — It is a particular, built-in manner to make use of dropout to struggle overfitting in recurrent layers.
• Stacking recurrent layers — This will increase the representational energy of the community (at the price of increased computational masses).
• Bidirectional recurrent layers — These current the identical data to a recurrent community in several methods, rising accuracy and mitigating forgetting points.

A temperature-forecasting drawback

Till now, the one sequence knowledge we’ve lined has been textual content knowledge, such because the IMDB dataset and the Reuters dataset. However sequence knowledge is discovered in lots of extra issues than simply language processing. In all of the examples on this part, you’ll play with a climate timeseries dataset recorded on the Climate Station on the Max Planck Institute for Biogeochemistry in Jena, Germany.

On this dataset, 14 completely different portions (such air temperature, atmospheric stress, humidity, wind route, and so forth) have been recorded each 10 minutes, over a number of years. The unique knowledge goes again to 2003, however this instance is proscribed to knowledge from 2009–2016. This dataset is ideal for studying to work with numerical time collection. You’ll use it to construct a mannequin that takes as enter some knowledge from the latest previous (a number of days’ value of knowledge factors) and predicts the air temperature 24 hours sooner or later.

Obtain and uncompress the info as follows:

dir.create("~/Downloads/jena_climate", recursive = TRUE)
obtain.file(
  "https://s3.amazonaws.com/keras-datasets/jena_climate_2009_2016.csv.zip",
  "~/Downloads/jena_climate/jena_climate_2009_2016.csv.zip"
)
unzip(
  "~/Downloads/jena_climate/jena_climate_2009_2016.csv.zip",
  exdir = "~/Downloads/jena_climate"
)

Let’s take a look at the info.

Observations: 420,551
Variables: 15
$ `Date Time`       <chr> "01.01.2009 00:10:00", "01.01.2009 00:20:00", "...
$ `p (mbar)`        <dbl> 996.52, 996.57, 996.53, 996.51, 996.51, 996.50,...
$ `T (degC)`        <dbl> -8.02, -8.41, -8.51, -8.31, -8.27, -8.05, -7.62...
$ `Tpot (Okay)`        <dbl> 265.40, 265.01, 264.91, 265.12, 265.15, 265.38,...
$ `Tdew (degC)`     <dbl> -8.90, -9.28, -9.31, -9.07, -9.04, -8.78, -8.30...
$ `rh (%)`          <dbl> 93.3, 93.4, 93.9, 94.2, 94.1, 94.4, 94.8, 94.4,...
$ `VPmax (mbar)`    <dbl> 3.33, 3.23, 3.21, 3.26, 3.27, 3.33, 3.44, 3.44,...
$ `VPact (mbar)`    <dbl> 3.11, 3.02, 3.01, 3.07, 3.08, 3.14, 3.26, 3.25,...
$ `VPdef (mbar)`    <dbl> 0.22, 0.21, 0.20, 0.19, 0.19, 0.19, 0.18, 0.19,...
$ `sh (g/kg)`       <dbl> 1.94, 1.89, 1.88, 1.92, 1.92, 1.96, 2.04, 2.03,...
$ `H2OC (mmol/mol)` <dbl> 3.12, 3.03, 3.02, 3.08, 3.09, 3.15, 3.27, 3.26,...
$ `rho (g/m**3)`    <dbl> 1307.75, 1309.80, 1310.24, 1309.19, 1309.00, 13...
$ `wv (m/s)`        <dbl> 1.03, 0.72, 0.19, 0.34, 0.32, 0.21, 0.18, 0.19,...
$ `max. wv (m/s)`   <dbl> 1.75, 1.50, 0.63, 0.50, 0.63, 0.63, 0.63, 0.50,...
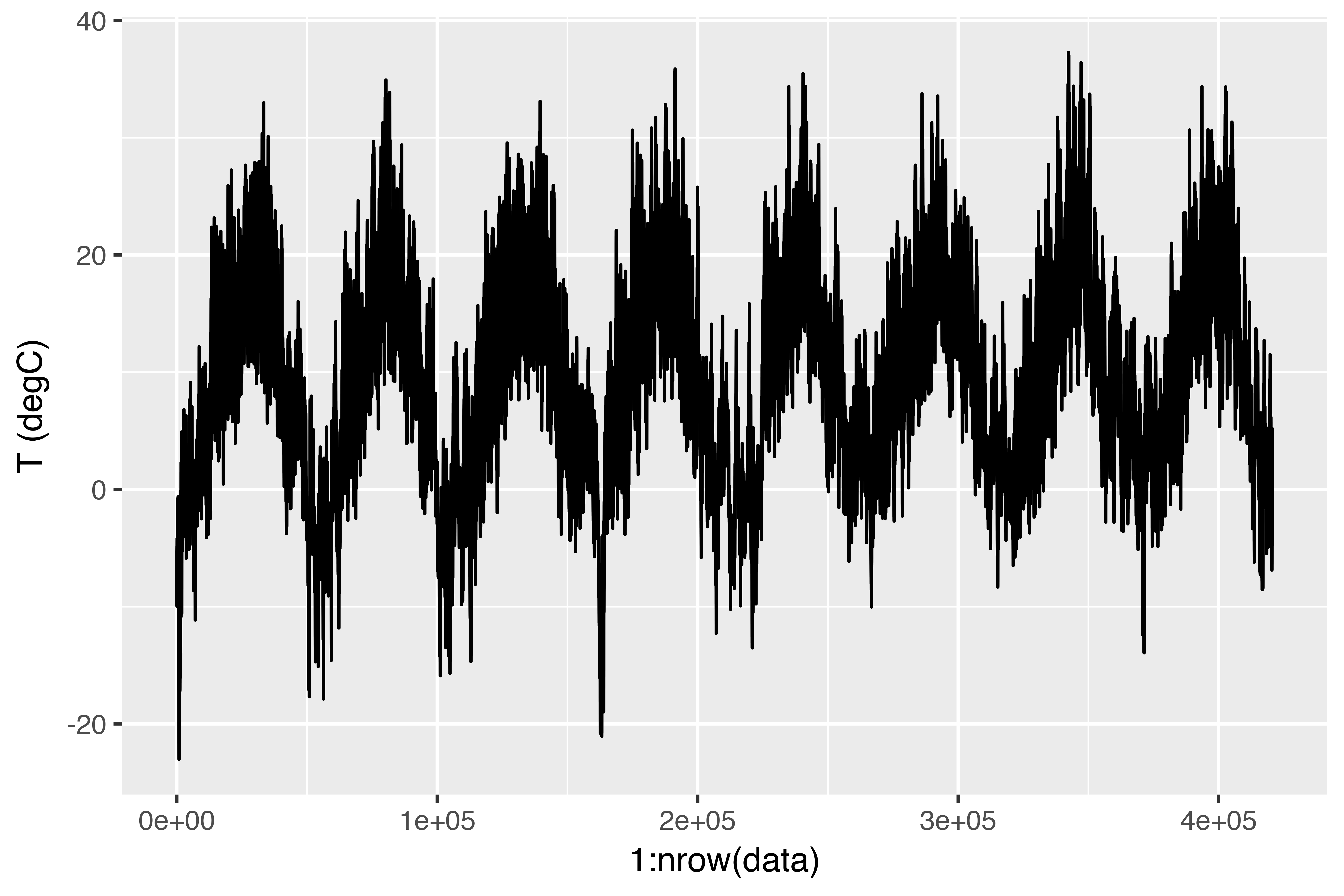
$ `wd (deg)`        <dbl> 152.3, 136.1, 171.6, 198.0, 214.3, 192.7, 166.5...

Right here is the plot of temperature (in levels Celsius) over time. On this plot, you’ll be able to clearly see the yearly periodicity of temperature.

Here’s a extra slim plot of the primary 10 days of temperature knowledge (see determine 6.15). As a result of the info is recorded each 10 minutes, you get 144 knowledge factors
per day.

ggplot(knowledge[1:1440,], aes(x = 1:1440, y = `T (degC)`)) + geom_line()

On this plot, you’ll be able to see every day periodicity, particularly evident for the final 4 days. Additionally be aware that this 10-day interval have to be coming from a reasonably chilly winter month.

If you happen to have been making an attempt to foretell common temperature for the subsequent month given a number of months of previous knowledge, the issue could be simple, because of the dependable year-scale periodicity of the info. However wanting on the knowledge over a scale of days, the temperature appears to be like much more chaotic. Is that this time collection predictable at a every day scale? Let’s discover out.

Making ready the info

The precise formulation of the issue shall be as follows: given knowledge going way back to lookback timesteps (a timestep is 10 minutes) and sampled each steps timesteps, can you expect the temperature in delay timesteps? You’ll use the next parameter values:

• lookback = 1440 — Observations will return 10 days.
• steps = 6 — Observations shall be sampled at one knowledge level per hour.
• delay = 144 — Targets shall be 24 hours sooner or later.

To get began, you could do two issues:

• Preprocess the info to a format a neural community can ingest. That is simple: the info is already numerical, so that you don’t have to do any vectorization. However every time collection within the knowledge is on a distinct scale (for instance, temperature is often between -20 and +30, however atmospheric stress, measured in mbar, is round 1,000). You’ll normalize every time collection independently in order that all of them take small values on the same scale.
• Write a generator operate that takes the present array of float knowledge and yields batches of knowledge from the latest previous, together with a goal temperature sooner or later. As a result of the samples within the dataset are extremely redundant (pattern N and pattern N + 1 could have most of their timesteps in widespread), it could be wasteful to explicitly allocate each pattern. As a substitute, you’ll generate the samples on the fly utilizing the unique knowledge.

sequence_generator <- operate(begin) {
  worth <- begin - 1
  operate() {
    worth <<- worth + 1
    worth
  }
}

gen <- sequence_generator(10)
gen()

[1] 10

[1] 11

First, you’ll convert the R knowledge body which we learn earlier right into a matrix of floating level values (we’ll discard the primary column which included a textual content timestamp):

You’ll then preprocess the info by subtracting the imply of every time collection and dividing by the usual deviation. You’re going to make use of the primary 200,000 timesteps as coaching knowledge, so compute the imply and normal deviation for normalization solely on this fraction of the info.

train_data <- knowledge[1:200000,]
imply <- apply(train_data, 2, imply)
std <- apply(train_data, 2, sd)
knowledge <- scale(knowledge, heart = imply, scale = std)

The code for the info generator you’ll use is beneath. It yields a listing (samples, targets), the place samples is one batch of enter knowledge and targets is the corresponding array of goal temperatures. It takes the next arguments:

• knowledge — The unique array of floating-point knowledge, which you normalized in itemizing 6.32.
• lookback — What number of timesteps again the enter knowledge ought to go.
• delay — What number of timesteps sooner or later the goal must be.
• min_index and max_index — Indices within the knowledge array that delimit which timesteps to attract from. That is helpful for protecting a section of the info for validation and one other for testing.
• shuffle — Whether or not to shuffle the samples or draw them in chronological order.
• batch_size — The variety of samples per batch.
• step — The interval, in timesteps, at which you pattern knowledge. You’ll set it 6 with a purpose to draw one knowledge level each hour.

generator <- operate(knowledge, lookback, delay, min_index, max_index,
                      shuffle = FALSE, batch_size = 128, step = 6) {
  if (is.null(max_index))
    max_index <- nrow(knowledge) - delay - 1
  i <- min_index + lookback
  operate() {
    if (shuffle) {
      rows <- pattern(c((min_index+lookback):max_index), measurement = batch_size)
    } else {
      if (i + batch_size >= max_index)
        i <<- min_index + lookback
      rows <- c(i:min(i+batch_size-1, max_index))
      i <<- i + size(rows)
    }

    samples <- array(0, dim = c(size(rows),
                                lookback / step,
                                dim(knowledge)[[-1]]))
    targets <- array(0, dim = c(size(rows)))
                      
    for (j in 1:size(rows)) {
      indices <- seq(rows[[j]] - lookback, rows[[j]]-1,
                     size.out = dim(samples)[[2]])
      samples[j,,] <- knowledge[indices,]
      targets[[j]] <- knowledge[rows[[j]] + delay,2]
    }           
    checklist(samples, targets)
  }
}

The i variable accommodates the state that tracks subsequent window of knowledge to return, so it’s up to date utilizing superassignment (e.g. i <<- i + size(rows)).

Now, let’s use the summary generator operate to instantiate three mills: one for coaching, one for validation, and one for testing. Every will take a look at completely different temporal segments of the unique knowledge: the coaching generator appears to be like on the first 200,000 timesteps, the validation generator appears to be like on the following 100,000, and the take a look at generator appears to be like on the the rest.

lookback <- 1440
step <- 6
delay <- 144
batch_size <- 128

train_gen <- generator(
  knowledge,
  lookback = lookback,
  delay = delay,
  min_index = 1,
  max_index = 200000,
  shuffle = TRUE,
  step = step, 
  batch_size = batch_size
)

val_gen = generator(
  knowledge,
  lookback = lookback,
  delay = delay,
  min_index = 200001,
  max_index = 300000,
  step = step,
  batch_size = batch_size
)

test_gen <- generator(
  knowledge,
  lookback = lookback,
  delay = delay,
  min_index = 300001,
  max_index = NULL,
  step = step,
  batch_size = batch_size
)

# What number of steps to attract from val_gen with a purpose to see your complete validation set
val_steps <- (300000 - 200001 - lookback) / batch_size

# What number of steps to attract from test_gen with a purpose to see your complete take a look at set
test_steps <- (nrow(knowledge) - 300001 - lookback) / batch_size

A standard-sense, non-machine-learning baseline

Earlier than you begin utilizing black-box deep-learning fashions to unravel the temperature-prediction drawback, let’s strive a easy, commonsense strategy. It’ll function a sanity test, and it’ll set up a baseline that you just’ll should beat with a purpose to display the usefulness of more-advanced machine-learning fashions. Such commonsense baselines could be helpful whenever you’re approaching a brand new drawback for which there isn’t a recognized resolution (but). A traditional instance is that of unbalanced classification duties, the place some courses are way more widespread than others. In case your dataset accommodates 90% situations of sophistication A and 10% situations of sophistication B, then a commonsense strategy to the classification job is to all the time predict “A” when offered with a brand new pattern. Such a classifier is 90% correct general, and any learning-based strategy ought to due to this fact beat this 90% rating with a purpose to display usefulness. Typically, such elementary baselines can show surprisingly onerous to beat.

On this case, the temperature time collection can safely be assumed to be steady (the temperatures tomorrow are more likely to be near the temperatures right this moment) in addition to periodical with a every day interval. Thus a commonsense strategy is to all the time predict that the temperature 24 hours from now shall be equal to the temperature proper now. Let’s consider this strategy, utilizing the imply absolute error (MAE) metric:

Right here’s the analysis loop.

library(keras)
evaluate_naive_method <- operate() {
  batch_maes <- c()
  for (step in 1:val_steps) {
    c(samples, targets) %<-% val_gen()
    preds <- samples[,dim(samples)[[2]],2]
    mae <- imply(abs(preds - targets))
    batch_maes <- c(batch_maes, mae)
  }
  print(imply(batch_maes))
}

evaluate_naive_method()

This yields an MAE of 0.29. As a result of the temperature knowledge has been normalized to be centered on 0 and have an ordinary deviation of 1, this quantity isn’t instantly interpretable. It interprets to a mean absolute error of 0.29 x temperature_std levels Celsius: 2.57˚C.

celsius_mae <- 0.29 * std[[2]]

That’s a pretty big common absolute error. Now the sport is to make use of your information of deep studying to do higher.

A fundamental machine-learning strategy

In the identical manner that it’s helpful to determine a commonsense baseline earlier than making an attempt machine-learning approaches, it’s helpful to strive easy, low cost machine-learning fashions (akin to small, densely linked networks) earlier than wanting into sophisticated and computationally costly fashions akin to RNNs. That is one of the simplest ways to verify any additional complexity you throw on the drawback is reputable and delivers actual advantages.

The next itemizing reveals a totally linked mannequin that begins by flattening the info after which runs it via two dense layers. Notice the shortage of activation operate on the final dense layer, which is typical for a regression drawback. You employ MAE because the loss. Since you consider on the very same knowledge and with the very same metric you probably did with the commonsense strategy, the outcomes shall be straight comparable.

library(keras)

mannequin <- keras_model_sequential() %>% 
  layer_flatten(input_shape = c(lookback / step, dim(knowledge)[-1])) %>% 
  layer_dense(models = 32, activation = "relu") %>% 
  layer_dense(models = 1)

mannequin %>% compile(
  optimizer = optimizer_rmsprop(),
  loss = "mae"
)

historical past <- mannequin %>% fit_generator(
  train_gen,
  steps_per_epoch = 500,
  epochs = 20,
  validation_data = val_gen,
  validation_steps = val_steps
)

Let’s show the loss curves for validation and coaching.

A number of the validation losses are near the no-learning baseline, however not reliably. This goes to indicate the advantage of getting this baseline within the first place: it seems to be not simple to outperform. Your widespread sense accommodates a number of worthwhile data {that a} machine-learning mannequin doesn’t have entry to.

You could marvel, if a easy, well-performing mannequin exists to go from the info to the targets (the commonsense baseline), why doesn’t the mannequin you’re coaching discover it and enhance on it? As a result of this easy resolution isn’t what your coaching setup is in search of. The area of fashions by which you’re trying to find an answer – that’s, your speculation area – is the area of all potential two-layer networks with the configuration you outlined. These networks are already pretty sophisticated. Once you’re in search of an answer with an area of sophisticated fashions, the straightforward, well-performing baseline could also be unlearnable, even when it’s technically a part of the speculation area. That may be a fairly important limitation of machine studying normally: except the educational algorithm is hardcoded to search for a selected form of easy mannequin, parameter studying can generally fail to discover a easy resolution to a easy drawback.

A primary recurrent baseline

The primary totally linked strategy didn’t do nicely, however that doesn’t imply machine studying isn’t relevant to this drawback. The earlier strategy first flattened the time collection, which eliminated the notion of time from the enter knowledge. Let’s as a substitute take a look at the info as what it’s: a sequence, the place causality and order matter. You’ll strive a recurrent-sequence processing mannequin – it must be the right match for such sequence knowledge, exactly as a result of it exploits the temporal ordering of knowledge factors, in contrast to the primary strategy.

As a substitute of the LSTM layer launched within the earlier part, you’ll use the GRU layer, developed by Chung et al. in 2014. Gated recurrent unit (GRU) layers work utilizing the identical precept as LSTM, however they’re considerably streamlined and thus cheaper to run (though they might not have as a lot representational energy as LSTM). This trade-off between computational expensiveness and representational energy is seen all over the place in machine studying.

mannequin <- keras_model_sequential() %>% 
  layer_gru(models = 32, input_shape = checklist(NULL, dim(knowledge)[[-1]])) %>% 
  layer_dense(models = 1)

mannequin %>% compile(
  optimizer = optimizer_rmsprop(),
  loss = "mae"
)

historical past <- mannequin %>% fit_generator(
  train_gen,
  steps_per_epoch = 500,
  epochs = 20,
  validation_data = val_gen,
  validation_steps = val_steps
)

The outcomes are plotted beneath. A lot better! You possibly can considerably beat the commonsense baseline, demonstrating the worth of machine studying in addition to the prevalence of recurrent networks in comparison with sequence-flattening dense networks on any such job.

The brand new validation MAE of ~0.265 (earlier than you begin considerably overfitting) interprets to a imply absolute error of two.35˚C after denormalization. That’s a stable achieve on the preliminary error of two.57˚C, however you most likely nonetheless have a little bit of a margin for enchancment.

Utilizing recurrent dropout to struggle overfitting

It’s evident from the coaching and validation curves that the mannequin is overfitting: the coaching and validation losses begin to diverge significantly after a number of epochs. You’re already acquainted with a traditional approach for preventing this phenomenon: dropout, which randomly zeros out enter models of a layer with a purpose to break happenstance correlations within the coaching knowledge that the layer is uncovered to. However methods to accurately apply dropout in recurrent networks isn’t a trivial query. It has lengthy been recognized that making use of dropout earlier than a recurrent layer hinders studying somewhat than serving to with regularization. In 2015, Yarin Gal, as a part of his PhD thesis on Bayesian deep studying, decided the correct manner to make use of dropout with a recurrent community: the identical dropout masks (the identical sample of dropped models) must be utilized at each timestep, as a substitute of a dropout masks that varies randomly from timestep to timestep. What’s extra, with a purpose to regularize the representations shaped by the recurrent gates of layers akin to layer_gru and layer_lstm, a temporally fixed dropout masks must be utilized to the internal recurrent activations of the layer (a recurrent dropout masks). Utilizing the identical dropout masks at each timestep permits the community to correctly propagate its studying error via time; a temporally random dropout masks would disrupt this error sign and be dangerous to the educational course of.

Yarin Gal did his analysis utilizing Keras and helped construct this mechanism straight into Keras recurrent layers. Each recurrent layer in Keras has two dropout-related arguments: dropout, a float specifying the dropout price for enter models of the layer, and recurrent_dropout, specifying the dropout price of the recurrent models. Let’s add dropout and recurrent dropout to the layer_gru and see how doing so impacts overfitting. As a result of networks being regularized with dropout all the time take longer to totally converge, you’ll prepare the community for twice as many epochs.

mannequin <- keras_model_sequential() %>% 
  layer_gru(models = 32, dropout = 0.2, recurrent_dropout = 0.2,
            input_shape = checklist(NULL, dim(knowledge)[[-1]])) %>% 
  layer_dense(models = 1)

mannequin %>% compile(
  optimizer = optimizer_rmsprop(),
  loss = "mae"
)

historical past <- mannequin %>% fit_generator(
  train_gen,
  steps_per_epoch = 500,
  epochs = 40,
  validation_data = val_gen,
  validation_steps = val_steps
)

The plot beneath reveals the outcomes. Success! You’re not overfitting through the first 20 epochs. However though you could have extra steady analysis scores, your finest scores aren’t a lot decrease than they have been beforehand.

Stacking recurrent layers

Since you’re not overfitting however appear to have hit a efficiency bottleneck, you must think about rising the capability of the community. Recall the outline of the common machine-learning workflow: it’s typically a good suggestion to extend the capability of your community till overfitting turns into the first impediment (assuming you’re already taking fundamental steps to mitigate overfitting, akin to utilizing dropout). So long as you aren’t overfitting too badly, you’re possible underneath capability.

Growing community capability is often executed by rising the variety of models within the layers or including extra layers. Recurrent layer stacking is a traditional approach to construct more-powerful recurrent networks: for example, what presently powers the Google Translate algorithm is a stack of seven massive LSTM layers – that’s large.

To stack recurrent layers on high of one another in Keras, all intermediate layers ought to return their full sequence of outputs (a 3D tensor) somewhat than their output on the final timestep. That is executed by specifying return_sequences = TRUE.

mannequin <- keras_model_sequential() %>% 
  layer_gru(models = 32, 
            dropout = 0.1, 
            recurrent_dropout = 0.5,
            return_sequences = TRUE,
            input_shape = checklist(NULL, dim(knowledge)[[-1]])) %>% 
  layer_gru(models = 64, activation = "relu",
            dropout = 0.1,
            recurrent_dropout = 0.5) %>% 
  layer_dense(models = 1)

mannequin %>% compile(
  optimizer = optimizer_rmsprop(),
  loss = "mae"
)

historical past <- mannequin %>% fit_generator(
  train_gen,
  steps_per_epoch = 500,
  epochs = 40,
  validation_data = val_gen,
  validation_steps = val_steps
)

The determine beneath reveals the outcomes. You possibly can see that the added layer does enhance the outcomes a bit, although not considerably. You possibly can draw two conclusions:

• Since you’re nonetheless not overfitting too badly, you might safely improve the dimensions of your layers in a quest for validation-loss enchancment. This has a non-negligible computational value, although.
• Including a layer didn’t assist by a major issue, so you might be seeing diminishing returns from rising community capability at this level.

Utilizing bidirectional RNNs

The final approach launched on this part known as bidirectional RNNs. A bidirectional RNN is a typical RNN variant that may supply higher efficiency than an everyday RNN on sure duties. It’s often utilized in natural-language processing – you might name it the Swiss Military knife of deep studying for natural-language processing.

RNNs are notably order dependent, or time dependent: they course of the timesteps of their enter sequences so as, and shuffling or reversing the timesteps can utterly change the representations the RNN extracts from the sequence. That is exactly the rationale they carry out nicely on issues the place order is significant, such because the temperature-forecasting drawback. A bidirectional RNN exploits the order sensitivity of RNNs: it consists of utilizing two common RNNs, such because the layer_gru and layer_lstm you’re already acquainted with, every of which processes the enter sequence in a single route (chronologically and antichronologically), after which merging their representations. By processing a sequence each methods, a bidirectional RNN can catch patterns that could be missed by a unidirectional RNN.

Remarkably, the truth that the RNN layers on this part have processed sequences in chronological order (older timesteps first) might have been an arbitrary choice. Not less than, it’s a choice we made no try to query to this point. May the RNNs have carried out nicely sufficient in the event that they processed enter sequences in antichronological order, for example (newer timesteps first)? Let’s do this in observe and see what occurs. All you could do is write a variant of the info generator the place the enter sequences are reverted alongside the time dimension (exchange the final line with checklist(samples[,ncol(samples):1,], targets)). Coaching the identical one-GRU-layer community that you just used within the first experiment on this part, you get the outcomes proven beneath.

The reversed-order GRU underperforms even the commonsense baseline, indicating that on this case, chronological processing is essential to the success of your strategy. This makes good sense: the underlying GRU layer will sometimes be higher at remembering the latest previous than the distant previous, and naturally the newer climate knowledge factors are extra predictive than older knowledge factors for the issue (that’s what makes the commonsense baseline pretty robust). Thus the chronological model of the layer is sure to outperform the reversed-order model. Importantly, this isn’t true for a lot of different issues, together with pure language: intuitively, the significance of a phrase in understanding a sentence isn’t often depending on its place within the sentence. Let’s strive the identical trick on the LSTM IMDB instance from part 6.2.

library(keras)

# Variety of phrases to think about as options
max_features <- 10000  

# Cuts off texts after this variety of phrases
maxlen <- 500

imdb <- dataset_imdb(num_words = max_features)
c(c(x_train, y_train), c(x_test, y_test)) %<-% imdb

# Reverses sequences
x_train <- lapply(x_train, rev)
x_test <- lapply(x_test, rev) 

# Pads sequences
x_train <- pad_sequences(x_train, maxlen = maxlen)  <4>
x_test <- pad_sequences(x_test, maxlen = maxlen)

mannequin <- keras_model_sequential() %>% 
  layer_embedding(input_dim = max_features, output_dim = 128) %>% 
  layer_lstm(models = 32) %>% 
  layer_dense(models = 1, activation = "sigmoid")

mannequin %>% compile(
  optimizer = "rmsprop",
  loss = "binary_crossentropy",
  metrics = c("acc")
)
  
historical past <- mannequin %>% match(
  x_train, y_train,
  epochs = 10,
  batch_size = 128,
  validation_split = 0.2
)

mannequin <- keras_model_sequential() %>% 
  layer_embedding(input_dim = max_features, output_dim = 32) %>% 
  bidirectional(
    layer_lstm(models = 32)
  ) %>% 
  layer_dense(models = 1, activation = "sigmoid")

mannequin %>% compile(
  optimizer = "rmsprop",
  loss = "binary_crossentropy",
  metrics = c("acc")
)

historical past <- mannequin %>% match(
  x_train, y_train,
  epochs = 10,
  batch_size = 128,
  validation_split = 0.2
)

It performs barely higher than the common LSTM you tried within the earlier part, reaching over 89% validation accuracy. It additionally appears to overfit extra shortly, which is unsurprising as a result of a bidirectional layer has twice as many parameters as a chronological LSTM. With some regularization, the bidirectional strategy would possible be a robust performer on this job.

Now let’s strive the identical strategy on the temperature prediction job.

mannequin <- keras_model_sequential() %>% 
  bidirectional(
    layer_gru(models = 32), input_shape = checklist(NULL, dim(knowledge)[[-1]])
  ) %>% 
  layer_dense(models = 1)

mannequin %>% compile(
  optimizer = optimizer_rmsprop(),
  loss = "mae"
)

historical past <- mannequin %>% fit_generator(
  train_gen,
  steps_per_epoch = 500,
  epochs = 40,
  validation_data = val_gen,
  validation_steps = val_steps
)

This performs about in addition to the common layer_gru. It’s simple to know why: all of the predictive capability should come from the chronological half of the community, as a result of the antichronological half is thought to be severely underperforming on this job (once more, as a result of the latest previous issues way more than the distant previous on this case).

Going even additional

There are lots of different issues you might strive, with a purpose to enhance efficiency on the temperature-forecasting drawback:

• Regulate the variety of models in every recurrent layer within the stacked setup. The present selections are largely arbitrary and thus most likely suboptimal.
• Regulate the educational price utilized by the RMSprop optimizer.
• Attempt utilizing layer_lstm as a substitute of layer_gru.
• Attempt utilizing an even bigger densely linked regressor on high of the recurrent layers: that’s, an even bigger dense layer or perhaps a stack of dense layers.
• Don’t neglect to ultimately run the best-performing fashions (when it comes to validation MAE) on the take a look at set! In any other case, you’ll develop architectures which are overfitting to the validation set.

As all the time, deep studying is extra an artwork than a science. We will present pointers that counsel what’s more likely to work or not work on a given drawback, however, finally, each drawback is exclusive; you’ll have to guage completely different methods empirically. There’s presently no principle that can let you know prematurely exactly what you must do to optimally resolve an issue. You could iterate.

Wrapping up

Right here’s what you must take away from this part:

• As you first discovered in chapter 4, when approaching a brand new drawback, it’s good to first set up commonsense baselines to your metric of selection. If you happen to don’t have a baseline to beat, you’ll be able to’t inform whether or not you’re making actual progress.
• Attempt easy fashions earlier than costly ones, to justify the extra expense. Typically a easy mannequin will change into your best choice.
• When you could have knowledge the place temporal ordering issues, recurrent networks are an excellent match and simply outperform fashions that first flatten the temporal knowledge.
• To make use of dropout with recurrent networks, you must use a time-constant dropout masks and recurrent dropout masks. These are constructed into Keras recurrent layers, so all you must do is use the dropout and recurrent_dropout arguments of recurrent layers.
• Stacked RNNs present extra representational energy than a single RNN layer. They’re additionally way more costly and thus not all the time value it. Though they provide clear beneficial properties on complicated issues (akin to machine translation), they might not all the time be related to smaller, less complicated issues.
• Bidirectional RNNs, which take a look at a sequence each methods, are helpful on natural-language processing issues. However they aren’t robust performers on sequence knowledge the place the latest previous is way more informative than the start of the sequence.