When organizations got down to construct machine studying (ML) purposes corresponding to pure language processing (NLP) programs, advice engines, or search-based programs, typically occasions k-Nearest Neighbor (k-NN) search will probably be used in some unspecified time in the future within the workflow. Because the variety of information factors reaches the lots of of hundreds of thousands and even billions, scaling a k-NN search system could be a main problem. Making use of Approximate Nearest Neighbor (ANN) search is an effective way to beat this problem.
The k-NN drawback is comparatively easy in comparison with different ML strategies: given a set of factors and a question, discover the ok nearest factors within the set to the question. The naive answer is equally comprehensible: for every level within the set, compute its distance from the question and preserve monitor of the highest ok alongside the way in which.

The issue with this naive method is that it doesn’t scale notably effectively. The runtime search complexity is O(Nlogk), the place N is the variety of vectors and ok is the variety of nearest neighbors. Though this might not be noticeable when the set incorporates 1000’s of factors, it turns into noticeable when the dimensions will get into the hundreds of thousands. Though some actual k-NN algorithms can pace search up, they have a tendency to carry out equally to the naive method in larger dimensions.
Enter ANN search. We will scale back the runtime search latency if we loosen a number of constraints on the k-NN drawback:
- Enable indexing to take longer
- Enable extra space for use at question time
- Enable the search to return an approximation of the k-NN within the set
A number of completely different algorithms have been found to just do that.
OpenSearch is a community-driven, Apache 2.0-licensed, open-source search and analytics suite that makes it straightforward to ingest, search, visualize, and analyze information. The OpenSearch k-NN plugin offers the flexibility to make use of a few of these algorithms inside an OpenSearch cluster. On this submit, we focus on the completely different algorithms which are supported and run experiments to see among the trade-offs between them.
Hierarchical Navigable Small Worlds algorithm
The Hierarchical Navigable Small Worlds algorithm (HNSW) is among the hottest algorithms on the market for ANN search. It was the primary algorithm that the k-NN plugin supported, utilizing a really environment friendly implementation from the nmslib similarity search library. It has probably the greatest question latency vs. recall trade-offs and doesn’t require any coaching. The core thought of the algorithm is to construct a graph with edges connecting index vectors which are shut to one another. Then, on search, this graph is partially traversed to search out the approximate nearest neighbors to the question vector. To steer the traversal in direction of the question’s nearest neighbors, the algorithm all the time visits the closest candidate to the question vector subsequent.
However which vector ought to the traversal begin from? It may simply choose a random vector, however for a big index, this could be very removed from the question’s precise nearest neighbors, resulting in poor outcomes. To choose a vector that’s typically near the question vector to start out from, the algorithm builds not only one graph, however a hierarchy of graphs. All vectors are added to the underside layer, after which a random subset of these are added to the layer above, after which a subset of these are added to the layer above that, and so forth.
Throughout search, we begin from a random vector within the high layer, partially traverse the graph to search out (roughly) the closest level to the question vector in that layer, after which use this vector as the place to begin for our traversal of the layer beneath. We repeat this till we get to the underside layer. On the backside layer, we carry out the traversal, however this time, as an alternative of simply trying to find the closest neighbor, we preserve monitor of the k-nearest neighbors which are visited alongside the way in which.
The next determine illustrates this course of (impressed from the picture in authentic paper Environment friendly and sturdy approximate nearest neighbor search utilizing Hierarchical Navigable Small World graphs).
You possibly can tune three parameters for HNSW:
- m – The utmost variety of edges a vector will get in a graph. The upper this quantity is, the extra reminiscence the graph will eat, however the higher the search approximation could also be.
- ef_search – The scale of the queue of the candidate nodes to go to throughout traversal. When a node is visited, its neighbors are added to the queue to be visited sooner or later. When this queue is empty, the traversal will finish. A bigger worth will improve search latency, however could present higher search approximation.
- ef_construction – Similar to
ef_search. When a node is to be inserted into the graph, the algorithm will discover itsmedges by querying the graph with the brand new node because the question vector. This parameter controls the candidate queue measurement for this traversal. A bigger worth will improve index latency, however could present a greater search approximation.
For extra data on HNSW, you may learn by way of the paper Environment friendly and sturdy approximate nearest neighbor search utilizing Hierarchical Navigable Small World graphs.
Reminiscence consumption
Though HNSW offers superb approximate nearest neighbor search at low latencies, it will probably eat a considerable amount of reminiscence. Every HNSW graph makes use of roughly 1.1 * (4 * d + 8 * m) * num_vectors bytes of reminiscence:
dis the dimension of the vectorsmis the algorithm parameter that controls the variety of connections every node can have in a layernum_vectorsis the variety of vectors within the index
To make sure sturdiness and availability, particularly when operating manufacturing workloads, OpenSearch indexes are really useful to have at the very least one duplicate shard. Subsequently, the reminiscence requirement is multiplied by (1 + variety of replicas). To be used circumstances the place the information measurement is 1 billion vectors of 128 dimensions every and m is ready to the default worth of 16, the estimated quantity of reminiscence required can be:
1.1 * (4 * 128 + 8 * 16) * 1,000,000,000 * 2 = 1,408 GB.
If we improve the dimensions of vectors to 512, for instance, and the m to 100, which is really useful for vectors with excessive intrinsic dimensionality, some use circumstances can require a complete reminiscence of roughly 4 TB.
With OpenSearch, we are able to all the time horizontally scale the cluster to deal with this reminiscence requirement. Nevertheless, this comes on the expense of elevating infrastructure prices. For circumstances the place scaling doesn’t make sense, choices to cut back the reminiscence footprint of the k-NN system have to be explored. Fortuitously, there are algorithms that we are able to use to do that.
Inverted File System algorithm
Contemplate a special method for approximating a nearest neighbor search: separate your index vectors right into a set of buckets, then, to cut back your search time, solely search by way of a subset of those buckets. From a excessive stage, that is what the Inverted File System (IVF) ANN algorithm does. In OpenSearch 1.2, the k-NN plugin launched assist for the implementation of IVF by Faiss. Faiss is an open-sourced library from Meta for environment friendly similarity search and clustering of dense vectors.
Nevertheless, if we simply randomly cut up up our vectors into completely different buckets, and solely search a subset of them, this will probably be a poor approximation. The IVF algorithm makes use of a extra elegant method. First, earlier than indexing begins, it assigns every bucket a consultant vector. When a vector is listed, it will get added to the bucket that has the closest consultant vector. This fashion, vectors which are nearer to one another are positioned roughly in the identical or close by buckets.
To find out what the consultant vectors for the buckets are, the IVF algorithm requires a coaching step. On this step, k-Means clustering is run on a set of coaching information, and the centroids it produces turn into the consultant vectors. The next diagram illustrates this course of.
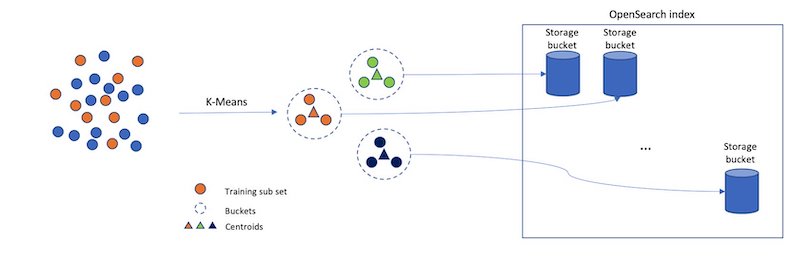
IVF has two parameters:
- nlist – The variety of buckets to create. Extra buckets will lead to longer coaching occasions, however could enhance the granularity of the search.
- nprobes – The variety of buckets to look. This parameter is pretty easy. The extra buckets which are searched, the longer the search will take, however the higher the approximation.
Reminiscence consumption
On the whole, IVF requires much less reminiscence than HNSW as a result of IVF doesn’t have to retailer a set of edges for every listed vector.
We estimate that IVF will roughly require the next quantity of reminiscence:
1.1 * (((4 * dimension) * num_vectors) + (4 * nlist * dimension)) bytes
For the case explored for HNSW the place there are 1,000,000,000 128-dimensional vectors with one layer of replication, an IVF algorithm with an nlist of 4096 would take roughly 1.1 * (((4 * 128) * 2,000,000,000) + (4 * 4096 * 128)) bytes = 1126 GB.
This financial savings does come at a value, nevertheless, as a result of HNSW gives a higher question latency versus approximation accuracy tradeoff.
Product quantization vector compression
Though you should use HNSW and IVF to hurry up nearest neighbor search, they’ll eat a substantial quantity of reminiscence. After we get into the billion-vector scale, we begin to require 1000’s of GBs of reminiscence to assist their index constructions. As we scale up the variety of vectors or the dimension of vectors, this requirement continues to develop. Is there a manner to make use of noticeably much less house for our k-NN index?
The reply is sure! In actual fact, there are plenty of alternative ways to cut back the quantity of reminiscence vectors require. You possibly can change your embedding mannequin to supply smaller vectors, or you may apply strategies like Precept Element Evaluation (PCA) to cut back the vector’s dimensionality. One other method is to make use of quantization. The final thought of vector quantization is to map a big vector house with steady values right into a smaller house with discrete values. When a vector is mapped right into a smaller house, it requires fewer bits to symbolize. Nevertheless, this comes at a value—when mapping to a smaller enter house, some details about the vector is misplaced.
Product quantization (PQ) is a extremely popular quantization method within the discipline of nearest neighbor search. It may be used along with ANN algorithms for nearest neighbor search. Together with IVF, the k-NN plugin added assist for Faiss’s PQ implementation in OpenSearch 1.2.
The principle thought of PQ is to interrupt up a vector into a number of sub-vectors and encode the sub-vectors independently with a hard and fast variety of bits. The variety of sub-vectors that the unique vector is damaged up into is managed by a parameter, m, and the variety of bits to encode every sub-vector with is managed by a parameter, code_size. After encoding finishes, a vector is compressed into roughly m * code_size bits. So, assume we’ve a set of 100,000 1024-dimensional vectors. With m = 8 and code_size = 8, PQ breaks every vector into 8 128-dimensional sub-vectors and encode every sub-vector with 8 bits.
The values used for encoding are produced throughout a coaching step. Throughout coaching, tables are created with 2code_size entries for every sub-vector partition. Subsequent, k-Means clustering, with a ok worth of 2code_size, is run on the corresponding partition of sub-vectors from the coaching information. The centroids produced listed below are added because the entries to the partition’s desk.
After all of the tables are created, we encode a vector by changing every sub-vector with the ID of the closest vector within the partition’s desk. Within the instance the place code_size = 8, we solely want 8 bits to retailer an ID as a result of there are 28 parts within the desk. So, with dimension = 1024 and m = 8, the full measurement of 1 vector (assuming it makes use of a 32-bit floating level information kind) is decreased from 4,096 bytes to roughly 8 bytes!

After we need to decode a vector, we are able to reconstruct an approximated model of it by utilizing the saved IDs to retrieve the vectors from every partition’s desk. The space from the question vector to the reconstructed vector can then be computed and utilized in a nearest neighbor search. (It’s price noting that, in apply, additional optimization strategies like ADC are used to hurry up this course of for k-NN search).
Reminiscence consumption
As we talked about earlier, PQ will encode every vector into roughly m * code_size bits plus some overhead for every vector.
When combining it with IVF, we are able to estimate the index measurement as follows:
1.1 * ((((code_size/8) * m + overhead_per_vector) * num_vectors) + (4 * nlist * dimension) + (2 code_size * 4 * dimension) bytes
Utilizing 1 billion vectors, dimension = 128, m = 8, code_size = 8, and nlist = 4096, we get an estimated whole reminiscence consumption of 70GB: 1.1 * ((((8 / 8) * 8 + 24) * 1,000,000,000) + (4 * 4096 * 128) + (2^8 * 4 * 128)) * 2 = 70 GB.
Operating k-NN with OpenSearch
First be sure you have an OpenSearch cluster up and operating. For directions, seek advice from Cluster formation. For a extra managed answer, you should use Amazon OpenSearch Service.
Earlier than entering into the experiments, let’s go over how you can run k-NN workloads in OpenSearch. First, we have to create an index. An index shops a set of paperwork in a manner that they are often simply searched. For k-NN, the index’s mapping tells OpenSearch what algorithms to make use of and what parameters to make use of with them. We begin by creating an index that makes use of HNSW as its search algorithm:
Within the settings, we have to allow knn in order that the index will be searched with the knn question kind (extra on this later). We additionally set the variety of shards, and the variety of replicas every shard can have. An index is made up of a group of shards. Sharding is how OpenSearch distributes an index throughout a number of nodes in a cluster. For extra details about shards, seek advice from Sizing Amazon OpenSearch Service domains.
Within the mappings, we configure a discipline referred to as my_vector of kind knn_vector to retailer the vector information. We additionally go nmslib because the engine to let OpenSearch comprehend it ought to use nmslib’s implementation of HNSW. Moreover, we go l2 because the space_type. The space_type determines the perform used to compute the gap between two vectors. l2 refers back to the Euclidean distance. OpenSearch additionally helps cosine similarity and the interior product distance features.
After the index is created, we are able to ingest some faux information:
After including some paperwork to the index, we are able to search it:
Creating an index that makes use of IVF or PQ is just a little bit completely different as a result of these algorithms require coaching. Earlier than creating the index, we have to create a mannequin utilizing the coaching API:
The training_index and training_field specify the place the coaching information is saved. The one requirement for the coaching information index is that it has a knn_vector discipline that has the identical dimension as you need your mannequin to have. The tactic defines the algorithm that ought to be used for search.
After the coaching request is submitted, it can run within the background. To examine if the coaching is full, you should use the GET mannequin API:
After the mannequin is created, you may create an index that makes use of this mannequin:
After the index is created, we are able to add paperwork to it and search it identical to we did for HNSW.
Experiments
Let’s run a number of experiments to see how these algorithms carry out in apply and what tradeoffs are made. We have a look at an HNSW versus an IVF index utilizing PQ. For these experiments, we’re serious about search accuracy, question latency, and reminiscence consumption. As a result of these trade-offs are primarily noticed at scale, we use the BIGANN dataset containing 1 billion vectors of 128 dimensions. The dataset additionally incorporates 10,000 queries of take a look at information mapping a question to the bottom fact closest 100 vectors based mostly on the Euclidean distance.
Particularly, we compute the next search metrics:
- Latency p99 (ms), Latency p90 (ms), Latency p50 (ms) – Question latency at varied quantiles in milliseconds
- recall@10 – The fraction of the highest 10 floor fact neighbors discovered within the 10 outcomes returned by the plugin
- Native reminiscence consumption (GB) – The quantity of reminiscence utilized by the plugin throughout querying
One factor to notice is that the BIGANN dataset makes use of an unsigned integer as the information kind. As a result of the knn_vector discipline doesn’t assist unsigned integers, the information is robotically transformed to floats.
To run the experiments, we full the next steps:
- Ingest the dataset into the cluster utilizing the OpenSearch Benchmarks framework (the code will be discovered on GitHub).
- When ingestion is full, we use the warmup API to organize the cluster for the search workload.
- We run the ten,000 take a look at queries in opposition to the cluster 10 occasions and acquire the aggregated outcomes.
The queries return the doc ID solely, and never the vector, to enhance efficiency (code for this may be discovered on GitHub).
Parameter choice
One tough facet of operating experiments is deciding on the parameters. There are too many alternative combos of parameters to check all of them. That being mentioned, we determined to create three configurations for HNSW and IVFPQ:
- Optimize for search latency and reminiscence
- Optimize for recall
- Fall someplace within the center
For every optimization technique, we selected two configurations.
For HNSW, we are able to tune the m, ef_construction, and ef_search parameters to attain our desired trade-off:
- m – Controls the utmost variety of edges a node in a graph can have. As a result of every node has to retailer all of its edges, rising this worth will improve the reminiscence footprint, but in addition improve the connectivity of the graph, which can enhance recall.
- ef_construction – Controls the dimensions of the candidate queue for edges when including a node to the graph. Growing this worth will improve the variety of candidates to contemplate, which can improve the index latency. Nevertheless, as a result of extra candidates will probably be thought-about, the standard of the graph will probably be higher, main to higher recall throughout search.
- ef_search – Just like
ef_construction, it controls the dimensions of the candidate queue for graph traversal throughout search. Growing this worth will improve the search latency, however may also enhance the recall.
On the whole, we selected configurations that steadily elevated the parameters, as detailed within the following desk.
| Config ID | Optimization Technique | m | ef_construction | ef_search |
| hnsw1 | Optimize for reminiscence and search latency | 8 | 32 | 32 |
| hnsw2 | Optimize for reminiscence and search latency | 16 | 32 | 32 |
| hnsw3 | Steadiness between latency, reminiscence, and recall | 16 | 128 | 128 |
| hnsw4 | Steadiness between latency, reminiscence, and recall | 32 | 256 | 256 |
| hnsw5 | Optimize for recall | 32 | 512 | 512 |
| hnsw6 | Optimize for recall | 64 | 512 | 512 |
For IVF, we are able to tune two parameters:
- nlist – Controls the granularity of the partitioning. The really useful worth for this parameter is a perform of the variety of vectors within the index. One factor to remember is that there are Faiss indexes that map to Lucene segments. There are a number of Lucene segments per shard and a number of other shards per OpenSearch index. For our estimates, we assumed that there can be 100 segments per shard and 24 shards, so about 420,000 vectors per Faiss index. With this worth, we estimated a great worth to be 4096 and saved this fixed for the experiments.
- nprobes – Controls the variety of nlist buckets we search. Increased values typically result in improved recollects on the expense of elevated search latencies.
For PQ, we are able to tune two parameters:
- m – Controls the variety of partitions to interrupt the vector into. The bigger this worth is, the higher the encoding will approximate the unique, on the expense of elevating reminiscence consumption.
- code_size – Controls the variety of bits to encode a sub-vector with. The bigger this worth is, the higher the encoding approximates the unique, on the expense of elevating reminiscence consumption. The max worth is 8, so we saved it fixed at 8 for all experiments.
The next desk summarizes our methods.
| Config ID | Optimization Technique | nprobes | m (num_sub_vectors) |
| ivfpq1 | Optimize for reminiscence and search latency | 8 | 8 |
| ivfpq2 | Optimize for reminiscence and search latency | 16 | 8 |
| ivfpq3 | Steadiness between latency, reminiscence, and recall | 32 | 16 |
| ivfpq4 | Steadiness between latency, reminiscence, and recall | 64 | 32 |
| ivfpq5 | Optimize for recall | 128 | 16 |
| ivfpq6 | Optimize for recall | 128 | 32 |
Moreover, we have to determine how a lot coaching information to make use of for IVFPQ. On the whole, Faiss recommends between 30,000 and 256,000 coaching vectors for parts involving k-Means coaching. For our configurations, the utmost ok for k-Means is 4096 from the nlist parameter. With this formulation, the really useful coaching set measurement is between 122,880 and 1,048,576 vectors, so we settled on 1 million vectors. The coaching information comes from the index vector dataset.
Lastly, for the index configurations, we have to choose the shard rely. It’s really useful to maintain the shard measurement between 10–50 GBs for OpenSearch. Experimentally, we decided that for HNSW, a great quantity can be 64 shards and for IVFPQ, 42. Each index configurations had been configured with one duplicate.
Cluster configuration
To run these experiments, we used Amazon OpenSearch Service utilizing model 1.3 of OpenSearch to create the clusters. We determined to make use of the r5 occasion household, which offers a great trade-off between reminiscence measurement and value.
The variety of nodes will rely upon the quantity of reminiscence that can be utilized for the algorithm per node and the full quantity of reminiscence required by the algorithm. Having extra nodes and extra reminiscence will typically enhance efficiency, however for these experiments, we need to decrease value. The quantity of reminiscence obtainable per node is computed as memory_available = (node_memory - jvm_size) * circuit_breaker_limit, with the next parameters:
- node_memory – The whole reminiscence of the occasion.
- jvm_size – The OpenSearch JVM heap measurement. Set to 32 GB.
- circuit_breaker_limit – The native reminiscence utilization threshold for the circuit breaker. Set to 0.5.
As a result of HNSW and IVFPQ have completely different reminiscence necessities, we estimate how a lot reminiscence is required for every algorithm and decide the required variety of nodes accordingly.
For HNSW, with m = 64, the full reminiscence required utilizing the formulation from the earlier sections is roughly 2,252 GB. Subsequently, with r5.12xlarge (384 GB of reminiscence), memory_available is 176 GB and the full variety of nodes required is about 12, which we spherical as much as 16 for stability functions.
As a result of the IVFPQ algorithm requires much less reminiscence, we are able to use a smaller occasion kind, the r5.4xlarge occasion, which has 128 GB of reminiscence. Subsequently, the memory_available for the algorithm is 48 GB. The estimated algorithm reminiscence consumption the place m = 64 is a complete of 193 GB and the full variety of nodes required is 4, which we spherical as much as six for stability functions.
For each clusters, we use c5.2xlarge occasion sorts as devoted chief nodes. This can present extra stability for the cluster.
Based on the AWS Pricing Calculator, for this explicit use case, the price per hour of the HNSW cluster is round $75 an hour, and the IVFPQ cluster prices round $11 an hour. That is essential to recollect when evaluating the outcomes.
Additionally, remember the fact that these benchmarks will be run utilizing your customized infrastructure, utilizing Amazon Elastic Compute Cloud (Amazon EC2), so long as the occasion sorts and their reminiscence measurement is equal.
Outcomes
The next tables summarize the outcomes from the experiments.
| Take a look at ID | p50 Question latency (ms) | p90 Question latency (ms) | p99 Question latency (ms) | Recall@10 | Native reminiscence consumption (GB) |
| hnsw1 | 9.1 | 11 | 16.9 | 0.84 | 1182 |
| hnsw2 | 11 | 12.1 | 17.8 | 0.93 | 1305 |
| hnsw3 | 23.1 | 27.1 | 32.2 | 0.99 | 1306 |
| hnsw4 | 54.1 | 68.3 | 80.2 | 0.99 | 1555 |
| hnsw5 | 83.4 | 100.6 | 114.7 | 0.99 | 1555 |
| hnsw6 | 103.7 | 131.8 | 151.7 | 0.99 | 2055 |
| Take a look at ID | p50 Question latency (ms) | p90 Question latency (ms) | p99 Question latency (ms) | Recall@10 | Native reminiscence consumption (GB) |
| ivfpq1 | 74.9 | 100.5 | 106.4 | 0.17 | 68 |
| ivfpq2 | 78.5 | 104.6 | 110.2 | 0.18 | 68 |
| ivfpq3 | 87.8 | 107 | 122 | 0.39 | 83 |
| ivfpq4 | 117.2 | 131.1 | 151.8 | 0.61 | 114 |
| ivfpq5 | 128.3 | 174.1 | 195.7 | 0.40 | 83 |
| ivfpq6 | 163 | 196.5 | 228.9 | 0.61 | 114 |
As you may count on, given what number of extra sources it makes use of, the HNSW cluster has decrease question latencies and higher recall. Nevertheless, the IVFPQ indexes use considerably much less reminiscence.
For HNSW, rising the parameters does in truth result in higher recall on the expense of latency. For IVFPQ, rising m has essentially the most important influence on bettering recall. Growing nprobes improves the recall marginally, however on the expense of great will increase in latencies.
Conclusion
On this submit, we lined completely different algorithms and strategies used to carry out approximate k-NN search at scale (over 1 billion information factors) inside OpenSearch. As we noticed within the earlier benchmarks part, there isn’t one algorithm or method that optimises for all of the metrics without delay. HNSW, IVF, and PQ every permit you to optimize for various metrics in your k-NN workload. When selecting the k-NN algorithm to make use of, first perceive the necessities of your use case (How correct does my approximate nearest neighbor search have to be? How briskly ought to or not it’s? What’s my finances?) after which tailor the algorithm configuration to satisfy them.
You possibly can check out the benchmarking code base we used on GitHub. You too can get began with approximate k-NN search at this time following the directions in Approximate k-NN search. For those who’re on the lookout for a managed answer in your OpenSearch cluster, take a look at Amazon OpenSearch Service.
Concerning the Authors
 Jack Mazanec is a software program engineer engaged on OpenSearch plugins. His major pursuits embrace machine studying and search engines like google. Exterior of labor, he enjoys snowboarding and watching sports activities.
Jack Mazanec is a software program engineer engaged on OpenSearch plugins. His major pursuits embrace machine studying and search engines like google. Exterior of labor, he enjoys snowboarding and watching sports activities.
 Othmane Hamzaoui is a Information Scientist working at AWS. He’s enthusiastic about fixing buyer challenges utilizing Machine Studying, with a deal with bridging the hole between analysis and enterprise to attain impactful outcomes. In his spare time, he enjoys operating and discovering new espresso outlets within the lovely metropolis of Paris.
Othmane Hamzaoui is a Information Scientist working at AWS. He’s enthusiastic about fixing buyer challenges utilizing Machine Studying, with a deal with bridging the hole between analysis and enterprise to attain impactful outcomes. In his spare time, he enjoys operating and discovering new espresso outlets within the lovely metropolis of Paris.




