Forecasting sunspots with deep studying
On this publish we’ll look at making time collection predictions utilizing the sunspots dataset that ships with base R. Sunspots are darkish spots on the solar, related to decrease temperature. Right here’s a picture from NASA exhibiting the photo voltaic phenomenon.

We’re utilizing the month-to-month model of the dataset, sunspots.month (there’s a yearly model, too).
It incorporates 265 years value of information (from 1749 by means of 2013) on the variety of sunspots monthly.

Forecasting this dataset is difficult due to excessive quick time period variability in addition to long-term irregularities evident within the cycles. For instance, most amplitudes reached by the low frequency cycle differ so much, as does the variety of excessive frequency cycle steps wanted to succeed in that most low frequency cycle top.
Our publish will give attention to two dominant facets: tips on how to apply deep studying to time collection forecasting, and tips on how to correctly apply cross validation on this area.
For the latter, we’ll use the rsample package deal that enables to do resampling on time collection information.
As to the previous, our purpose is to not attain utmost efficiency however to point out the overall plan of action when utilizing recurrent neural networks to mannequin this sort of information.
Recurrent neural networks
When our information has a sequential construction, it’s recurrent neural networks (RNNs) we use to mannequin it.
As of immediately, amongst RNNs, the perfect established architectures are the GRU (Gated Recurrent Unit) and the LSTM (Lengthy Quick Time period Reminiscence). For immediately, let’s not zoom in on what makes them particular, however on what they’ve in widespread with essentially the most stripped-down RNN: the essential recurrence construction.
In distinction to the prototype of a neural community, typically referred to as Multilayer Perceptron (MLP), the RNN has a state that’s carried on over time. That is properly seen on this diagram from Goodfellow et al., a.okay.a. the “bible of deep studying”:

At every time, the state is a mix of the present enter and the earlier hidden state. That is harking back to autoregressive fashions, however with neural networks, there must be some level the place we halt the dependence.
That’s as a result of with a purpose to decide the weights, we preserve calculating how our loss modifications because the enter modifications.
Now if the enter we now have to contemplate, at an arbitrary timestep, ranges again indefinitely – then we won’t be able to calculate all these gradients.
In follow, then, our hidden state will, at each iteration, be carried ahead by means of a set variety of steps.
We’ll come again to that as quickly as we’ve loaded and pre-processed the information.
Setup, pre-processing, and exploration
Libraries
Right here, first, are the libraries wanted for this tutorial.
If in case you have not beforehand run Keras in R, you’ll need to put in Keras utilizing the install_keras() operate.
# Set up Keras when you have not put in earlier than
install_keras()Knowledge
sunspot.month is a ts class (not tidy), so we’ll convert to a tidy information set utilizing the tk_tbl() operate from timetk. We use this as a substitute of as.tibble() from tibble to robotically protect the time collection index as a zoo yearmon index. Final, we’ll convert the zoo index to this point utilizing lubridate::as_date() (loaded with tidyquant) after which change to a tbl_time object to make time collection operations simpler.
sun_spots <- datasets::sunspot.month %>%
tk_tbl() %>%
mutate(index = as_date(index)) %>%
as_tbl_time(index = index)
sun_spots# A time tibble: 3,177 x 2
# Index: index
index worth
<date> <dbl>
1 1749-01-01 58
2 1749-02-01 62.6
3 1749-03-01 70
4 1749-04-01 55.7
5 1749-05-01 85
6 1749-06-01 83.5
7 1749-07-01 94.8
8 1749-08-01 66.3
9 1749-09-01 75.9
10 1749-10-01 75.5
# ... with 3,167 extra rowsExploratory information evaluation
The time collection is lengthy (265 years!). We will visualize the time collection each in full, and zoomed in on the primary 10 years to get a really feel for the collection.
Visualizing sunspot information with cowplot
We’ll make two ggplots and mix them utilizing cowplot::plot_grid(). Notice that for the zoomed in plot, we make use of tibbletime::time_filter(), which is a straightforward solution to carry out time-based filtering.
p1 <- sun_spots %>%
ggplot(aes(index, worth)) +
geom_point(coloration = palette_light()[[1]], alpha = 0.5) +
theme_tq() +
labs(
title = "From 1749 to 2013 (Full Knowledge Set)"
)
p2 <- sun_spots %>%
filter_time("begin" ~ "1800") %>%
ggplot(aes(index, worth)) +
geom_line(coloration = palette_light()[[1]], alpha = 0.5) +
geom_point(coloration = palette_light()[[1]]) +
geom_smooth(technique = "loess", span = 0.2, se = FALSE) +
theme_tq() +
labs(
title = "1749 to 1759 (Zoomed In To Present Modifications over the Yr)",
caption = "datasets::sunspot.month"
)
p_title <- ggdraw() +
draw_label("Sunspots", measurement = 18, fontface = "daring",
color = palette_light()[[1]])
plot_grid(p_title, p1, p2, ncol = 1, rel_heights = c(0.1, 1, 1))
Backtesting: time collection cross validation
When doing cross validation on sequential information, the time dependencies on previous samples should be preserved. We will create a cross validation sampling plan by offsetting the window used to pick out sequential sub-samples. In essence, we’re creatively coping with the truth that there’s no future check information obtainable by creating a number of artificial “futures” – a course of typically, esp. in finance, referred to as “backtesting”.
As talked about within the introduction, the rsample package deal consists of facitlities for backtesting on time collection. The vignette, “Time Sequence Evaluation Instance”, describes a process that makes use of the rolling_origin() operate to create samples designed for time collection cross validation. We’ll use this strategy.
Creating a backtesting technique
The sampling plan we create makes use of 100 years (preliminary = 12 x 100 samples) for the coaching set and 50 years (assess = 12 x 50) for the testing (validation) set. We choose a skip span of about 22 years (skip = 12 x 22 – 1) to roughly evenly distribute the samples into 6 units that span all the 265 years of sunspots historical past. Final, we choose cumulative = FALSE to permit the origin to shift which ensures that fashions on more moderen information aren’t given an unfair benefit (extra observations) over these working on much less current information. The tibble return incorporates the rolling_origin_resamples.
periods_train <- 12 * 100
periods_test <- 12 * 50
skip_span <- 12 * 22 - 1
rolling_origin_resamples <- rolling_origin(
sun_spots,
preliminary = periods_train,
assess = periods_test,
cumulative = FALSE,
skip = skip_span
)
rolling_origin_resamples# Rolling origin forecast resampling
# A tibble: 6 x 2
splits id
<checklist> <chr>
1 <S3: rsplit> Slice1
2 <S3: rsplit> Slice2
3 <S3: rsplit> Slice3
4 <S3: rsplit> Slice4
5 <S3: rsplit> Slice5
6 <S3: rsplit> Slice6Visualizing the backtesting technique
We will visualize the resamples with two customized features. The primary, plot_split(), plots one of many resampling splits utilizing ggplot2. Notice that an expand_y_axis argument is added to broaden the date vary to the complete sun_spots dataset date vary. This can develop into helpful once we visualize all plots collectively.
# Plotting operate for a single break up
plot_split <- operate(break up, expand_y_axis = TRUE,
alpha = 1, measurement = 1, base_size = 14) {
# Manipulate information
train_tbl <- coaching(break up) %>%
add_column(key = "coaching")
test_tbl <- testing(break up) %>%
add_column(key = "testing")
data_manipulated <- bind_rows(train_tbl, test_tbl) %>%
as_tbl_time(index = index) %>%
mutate(key = fct_relevel(key, "coaching", "testing"))
# Acquire attributes
train_time_summary <- train_tbl %>%
tk_index() %>%
tk_get_timeseries_summary()
test_time_summary <- test_tbl %>%
tk_index() %>%
tk_get_timeseries_summary()
# Visualize
g <- data_manipulated %>%
ggplot(aes(x = index, y = worth, coloration = key)) +
geom_line(measurement = measurement, alpha = alpha) +
theme_tq(base_size = base_size) +
scale_color_tq() +
labs(
title = glue("Cut up: {break up$id}"),
subtitle = glue("{train_time_summary$begin} to ",
"{test_time_summary$finish}"),
y = "", x = ""
) +
theme(legend.place = "none")
if (expand_y_axis) {
sun_spots_time_summary <- sun_spots %>%
tk_index() %>%
tk_get_timeseries_summary()
g <- g +
scale_x_date(limits = c(sun_spots_time_summary$begin,
sun_spots_time_summary$finish))
}
g
}The plot_split() operate takes one break up (on this case Slice01), and returns a visible of the sampling technique. We broaden the axis to the vary for the complete dataset utilizing expand_y_axis = TRUE.
rolling_origin_resamples$splits[[1]] %>%
plot_split(expand_y_axis = TRUE) +
theme(legend.place = "backside")
The second operate, plot_sampling_plan(), scales the plot_split() operate to all the samples utilizing purrr and cowplot.
# Plotting operate that scales to all splits
plot_sampling_plan <- operate(sampling_tbl, expand_y_axis = TRUE,
ncol = 3, alpha = 1, measurement = 1, base_size = 14,
title = "Sampling Plan") {
# Map plot_split() to sampling_tbl
sampling_tbl_with_plots <- sampling_tbl %>%
mutate(gg_plots = map(splits, plot_split,
expand_y_axis = expand_y_axis,
alpha = alpha, base_size = base_size))
# Make plots with cowplot
plot_list <- sampling_tbl_with_plots$gg_plots
p_temp <- plot_list[[1]] + theme(legend.place = "backside")
legend <- get_legend(p_temp)
p_body <- plot_grid(plotlist = plot_list, ncol = ncol)
p_title <- ggdraw() +
draw_label(title, measurement = 14, fontface = "daring",
color = palette_light()[[1]])
g <- plot_grid(p_title, p_body, legend, ncol = 1,
rel_heights = c(0.05, 1, 0.05))
g
}We will now visualize all the backtesting technique with plot_sampling_plan(). We will see how the sampling plan shifts the sampling window with every progressive slice of the practice/check splits.
rolling_origin_resamples %>%
plot_sampling_plan(expand_y_axis = T, ncol = 3, alpha = 1, measurement = 1, base_size = 10,
title = "Backtesting Technique: Rolling Origin Sampling Plan")
And, we will set expand_y_axis = FALSE to zoom in on the samples.
rolling_origin_resamples %>%
plot_sampling_plan(expand_y_axis = F, ncol = 3, alpha = 1, measurement = 1, base_size = 10,
title = "Backtesting Technique: Zoomed In")
We’ll use this backtesting technique (6 samples from one time collection every with 50/10 break up in years and a ~20 12 months offset) when testing the veracity of the LSTM mannequin on the sunspots dataset.
The LSTM mannequin
To start, we’ll develop an LSTM mannequin on a single pattern from the backtesting technique, specifically, the newest slice. We’ll then apply the mannequin to all samples to research modeling efficiency.
example_split <- rolling_origin_resamples$splits[[6]]
example_split_id <- rolling_origin_resamples$id[[6]]We will reuse the plot_split() operate to visualise the break up. Set expand_y_axis = FALSE to zoom in on the subsample.
plot_split(example_split, expand_y_axis = FALSE, measurement = 0.5) +
theme(legend.place = "backside") +
ggtitle(glue("Cut up: {example_split_id}"))
Knowledge setup
To assist hyperparameter tuning, in addition to the coaching set we additionally want a validation set.
For instance, we’ll use a callback, callback_early_stopping, that stops coaching when no vital efficiency is seen on the validation set (what’s thought of vital is as much as you).
We are going to dedicate 2 thirds of the evaluation set to coaching, and 1 third to validation.
df_trn <- evaluation(example_split)[1:800, , drop = FALSE]
df_val <- evaluation(example_split)[801:1200, , drop = FALSE]
df_tst <- evaluation(example_split)First, let’s mix the coaching and testing information units right into a single information set with a column key that specifies the place they got here from (both “coaching” or “testing)”. Notice that the tbl_time object might want to have the index respecified throughout the bind_rows() step, however this concern must be corrected in dplyr quickly.
df <- bind_rows(
df_trn %>% add_column(key = "coaching"),
df_val %>% add_column(key = "validation"),
df_tst %>% add_column(key = "testing")
) %>%
as_tbl_time(index = index)
df# A time tibble: 1,800 x 3
# Index: index
index worth key
<date> <dbl> <chr>
1 1849-06-01 81.1 coaching
2 1849-07-01 78 coaching
3 1849-08-01 67.7 coaching
4 1849-09-01 93.7 coaching
5 1849-10-01 71.5 coaching
6 1849-11-01 99 coaching
7 1849-12-01 97 coaching
8 1850-01-01 78 coaching
9 1850-02-01 89.4 coaching
10 1850-03-01 82.6 coaching
# ... with 1,790 extra rowsPreprocessing with recipes
The LSTM algorithm will often work higher if the enter information has been centered and scaled. We will conveniently accomplish this utilizing the recipes package deal. Along with step_center and step_scale, we’re utilizing step_sqrt to scale back variance and remov outliers. The precise transformations are executed once we bake the information in line with the recipe:
rec_obj <- recipe(worth ~ ., df) %>%
step_sqrt(worth) %>%
step_center(worth) %>%
step_scale(worth) %>%
prep()
df_processed_tbl <- bake(rec_obj, df)
df_processed_tbl# A tibble: 1,800 x 3
index worth key
<date> <dbl> <fct>
1 1849-06-01 0.714 coaching
2 1849-07-01 0.660 coaching
3 1849-08-01 0.473 coaching
4 1849-09-01 0.922 coaching
5 1849-10-01 0.544 coaching
6 1849-11-01 1.01 coaching
7 1849-12-01 0.974 coaching
8 1850-01-01 0.660 coaching
9 1850-02-01 0.852 coaching
10 1850-03-01 0.739 coaching
# ... with 1,790 extra rowsSubsequent, let’s seize the unique heart and scale so we will invert the steps after modeling. The sq. root step can then merely be undone by squaring the back-transformed information.
center_history <- rec_obj$steps[[2]]$means["value"]
scale_history <- rec_obj$steps[[3]]$sds["value"]
c("heart" = center_history, "scale" = scale_history)heart.worth scale.worth
6.694468 3.238935 Reshaping the information
Keras LSTM expects the enter in addition to the goal information to be in a selected form.
The enter must be a three-D array of measurement num_samples, num_timesteps, num_features.
Right here, num_samples is the variety of observations within the set. This can get fed to the mannequin in parts of batch_size. The second dimension, num_timesteps, is the size of the hidden state we have been speaking about above. Lastly, the third dimension is the variety of predictors we’re utilizing. For univariate time collection, that is 1.
How lengthy ought to we select the hidden state to be? This typically will depend on the dataset and our purpose.
If we did one-step-ahead forecasts – thus, forecasting the next month solely – our most important concern could be selecting a state size that enables to be taught any patterns current within the information.
Now say we needed to forecast 12 months as a substitute, as does SILSO, the World Knowledge Middle for the manufacturing, preservation and dissemination of the worldwide sunspot quantity.
The way in which we will do that, with Keras, is by wiring the LSTM hidden states to units of consecutive outputs of the identical size. Thus, if we need to produce predictions for 12 months, our LSTM ought to have a hidden state size of 12.
These 12 time steps will then get wired to 12 linear predictor models utilizing a time_distributed() wrapper.
That wrapper’s activity is to use the identical calculation (i.e., the identical weight matrix) to each state enter it receives.
Now, what’s the goal array’s format alleged to be? As we’re forecasting a number of timesteps right here, the goal information once more must be third-dimensional. Dimension 1 once more is the batch dimension, dimension 2 once more corresponds to the variety of timesteps (the forecasted ones), and dimension 3 is the dimensions of the wrapped layer.
In our case, the wrapped layer is a layer_dense() of a single unit, as we wish precisely one prediction per time limit.
So, let’s reshape the information. The primary motion right here is creating the sliding home windows of 12 steps of enter, adopted by 12 steps of output every. That is best to grasp with a shorter and less complicated instance. Say our enter have been the numbers from 1 to 10, and our chosen sequence size (state measurement) have been 4. Tthis is how we might need our coaching enter to look:
1,2,3,4
2,3,4,5
3,4,5,6And our goal information, correspondingly:
5,6,7,8
6,7,8,9
7,8,9,10We’ll outline a brief operate that does this reshaping on a given dataset.
Then lastly, we add the third axis that’s formally wanted (though that axis is of measurement 1 in our case).
# these variables are being outlined simply due to the order by which
# we current issues on this publish (first the information, then the mannequin)
# they are going to be outdated by FLAGS$n_timesteps, FLAGS$batch_size and n_predictions
# within the following snippet
n_timesteps <- 12
n_predictions <- n_timesteps
batch_size <- 10
# features used
build_matrix <- operate(tseries, overall_timesteps) {
t(sapply(1:(size(tseries) - overall_timesteps + 1), operate(x)
tseries[x:(x + overall_timesteps - 1)]))
}
reshape_X_3d <- operate(X) {
dim(X) <- c(dim(X)[1], dim(X)[2], 1)
X
}
# extract values from information body
train_vals <- df_processed_tbl %>%
filter(key == "coaching") %>%
choose(worth) %>%
pull()
valid_vals <- df_processed_tbl %>%
filter(key == "validation") %>%
choose(worth) %>%
pull()
test_vals <- df_processed_tbl %>%
filter(key == "testing") %>%
choose(worth) %>%
pull()
# construct the windowed matrices
train_matrix <-
build_matrix(train_vals, n_timesteps + n_predictions)
valid_matrix <-
build_matrix(valid_vals, n_timesteps + n_predictions)
test_matrix <- build_matrix(test_vals, n_timesteps + n_predictions)
# separate matrices into coaching and testing components
# additionally, discard final batch if there are fewer than batch_size samples
# (a purely technical requirement)
X_train <- train_matrix[, 1:n_timesteps]
y_train <- train_matrix[, (n_timesteps + 1):(n_timesteps * 2)]
X_train <- X_train[1:(nrow(X_train) %/% batch_size * batch_size), ]
y_train <- y_train[1:(nrow(y_train) %/% batch_size * batch_size), ]
X_valid <- valid_matrix[, 1:n_timesteps]
y_valid <- valid_matrix[, (n_timesteps + 1):(n_timesteps * 2)]
X_valid <- X_valid[1:(nrow(X_valid) %/% batch_size * batch_size), ]
y_valid <- y_valid[1:(nrow(y_valid) %/% batch_size * batch_size), ]
X_test <- test_matrix[, 1:n_timesteps]
y_test <- test_matrix[, (n_timesteps + 1):(n_timesteps * 2)]
X_test <- X_test[1:(nrow(X_test) %/% batch_size * batch_size), ]
y_test <- y_test[1:(nrow(y_test) %/% batch_size * batch_size), ]
# add on the required third axis
X_train <- reshape_X_3d(X_train)
X_valid <- reshape_X_3d(X_valid)
X_test <- reshape_X_3d(X_test)
y_train <- reshape_X_3d(y_train)
y_valid <- reshape_X_3d(y_valid)
y_test <- reshape_X_3d(y_test)Constructing the LSTM mannequin
Now that we now have our information within the required kind, let’s lastly construct the mannequin.
As at all times in deep studying, an necessary, and sometimes time-consuming, a part of the job is tuning hyperparameters. To maintain this publish self-contained, and contemplating that is primarily a tutorial on tips on how to use LSTM in R, let’s assume the next settings have been discovered after in depth experimentation (in actuality experimentation did happen, however to not a level that efficiency couldn’t probably be improved).
As a substitute of exhausting coding the hyperparameters, we’ll use tfruns to arrange an atmosphere the place we may simply carry out grid search.
We’ll rapidly touch upon what these parameters do however primarily depart these subjects to additional posts.
FLAGS <- flags(
# There's a so-called "stateful LSTM" in Keras. Whereas LSTM is stateful
# per se, this provides an additional tweak the place the hidden states get
# initialized with values from the merchandise at similar place within the earlier
# batch. That is useful just below particular circumstances, or in order for you
# to create an "infinite stream" of states, by which case you'd use 1 as
# the batch measurement. Beneath, we present how the code must be modified to
# use this, however it will not be additional mentioned right here.
flag_boolean("stateful", FALSE),
# Ought to we use a number of layers of LSTM?
# Once more, simply included for completeness, it didn't yield any superior
# efficiency on this activity.
# This can truly stack precisely one extra layer of LSTM models.
flag_boolean("stack_layers", FALSE),
# variety of samples fed to the mannequin in a single go
flag_integer("batch_size", 10),
# measurement of the hidden state, equals measurement of predictions
flag_integer("n_timesteps", 12),
# what number of epochs to coach for
flag_integer("n_epochs", 100),
# fraction of the models to drop for the linear transformation of the inputs
flag_numeric("dropout", 0.2),
# fraction of the models to drop for the linear transformation of the
# recurrent state
flag_numeric("recurrent_dropout", 0.2),
# loss operate. Discovered to work higher for this particular case than imply
# squared error
flag_string("loss", "logcosh"),
# optimizer = stochastic gradient descent. Appeared to work higher than adam
# or rmsprop right here (as indicated by restricted testing)
flag_string("optimizer_type", "sgd"),
# measurement of the LSTM layer
flag_integer("n_units", 128),
# studying charge
flag_numeric("lr", 0.003),
# momentum, a further parameter to the SGD optimizer
flag_numeric("momentum", 0.9),
# parameter to the early stopping callback
flag_integer("persistence", 10)
)
# the variety of predictions we'll make equals the size of the hidden state
n_predictions <- FLAGS$n_timesteps
# what number of options = predictors we now have
n_features <- 1
# simply in case we needed to strive totally different optimizers, we may add right here
optimizer <- change(FLAGS$optimizer_type,
sgd = optimizer_sgd(lr = FLAGS$lr,
momentum = FLAGS$momentum)
)
# callbacks to be handed to the match() operate
# We simply use one right here: we might cease earlier than n_epochs if the loss on the
# validation set doesn't lower (by a configurable quantity, over a
# configurable time)
callbacks <- checklist(
callback_early_stopping(persistence = FLAGS$persistence)
)In any case these preparations, the code for setting up and coaching the mannequin is moderately quick!
Let’s first rapidly view the “lengthy model”, that may will let you check stacking a number of LSTMs or use a stateful LSTM, then undergo the ultimate quick model (that does neither) and touch upon it.
This, only for reference, is the entire code.
mannequin <- keras_model_sequential()
mannequin %>%
layer_lstm(
models = FLAGS$n_units,
batch_input_shape = c(FLAGS$batch_size, FLAGS$n_timesteps, n_features),
dropout = FLAGS$dropout,
recurrent_dropout = FLAGS$recurrent_dropout,
return_sequences = TRUE,
stateful = FLAGS$stateful
)
if (FLAGS$stack_layers) {
mannequin %>%
layer_lstm(
models = FLAGS$n_units,
dropout = FLAGS$dropout,
recurrent_dropout = FLAGS$recurrent_dropout,
return_sequences = TRUE,
stateful = FLAGS$stateful
)
}
mannequin %>% time_distributed(layer_dense(models = 1))
mannequin %>%
compile(
loss = FLAGS$loss,
optimizer = optimizer,
metrics = checklist("mean_squared_error")
)
if (!FLAGS$stateful) {
mannequin %>% match(
x = X_train,
y = y_train,
validation_data = checklist(X_valid, y_valid),
batch_size = FLAGS$batch_size,
epochs = FLAGS$n_epochs,
callbacks = callbacks
)
} else {
for (i in 1:FLAGS$n_epochs) {
mannequin %>% match(
x = X_train,
y = y_train,
validation_data = checklist(X_valid, y_valid),
callbacks = callbacks,
batch_size = FLAGS$batch_size,
epochs = 1,
shuffle = FALSE
)
mannequin %>% reset_states()
}
}
if (FLAGS$stateful)
mannequin %>% reset_states()Now let’s step by means of the less complicated, but higher (or equally) performing configuration under.
# create the mannequin
mannequin <- keras_model_sequential()
# add layers
# we now have simply two, the LSTM and the time_distributed
mannequin %>%
layer_lstm(
models = FLAGS$n_units,
# the primary layer in a mannequin must know the form of the enter information
batch_input_shape = c(FLAGS$batch_size, FLAGS$n_timesteps, n_features),
dropout = FLAGS$dropout,
recurrent_dropout = FLAGS$recurrent_dropout,
# by default, an LSTM simply returns the ultimate state
return_sequences = TRUE
) %>% time_distributed(layer_dense(models = 1))
mannequin %>%
compile(
loss = FLAGS$loss,
optimizer = optimizer,
# along with the loss, Keras will inform us about present
# MSE whereas coaching
metrics = checklist("mean_squared_error")
)
historical past <- mannequin %>% match(
x = X_train,
y = y_train,
validation_data = checklist(X_valid, y_valid),
batch_size = FLAGS$batch_size,
epochs = FLAGS$n_epochs,
callbacks = callbacks
)As we see, coaching was stopped after ~55 epochs as validation loss didn’t lower any extra.
We additionally see that efficiency on the validation set is manner worse than efficiency on the coaching set – usually indicating overfitting.
This matter too, we’ll depart to a separate dialogue one other time, however curiously regularization utilizing increased values of dropout and recurrent_dropout (mixed with growing mannequin capability) didn’t yield higher generalization efficiency. That is most likely associated to the traits of this particular time collection we talked about within the introduction.
plot(historical past, metrics = "loss")
Now let’s see how properly the mannequin was in a position to seize the traits of the coaching set.
pred_train <- mannequin %>%
predict(X_train, batch_size = FLAGS$batch_size) %>%
.[, , 1]
# Retransform values to unique scale
pred_train <- (pred_train * scale_history + center_history) ^2
compare_train <- df %>% filter(key == "coaching")
# construct a dataframe that has each precise and predicted values
for (i in 1:nrow(pred_train)) {
varname <- paste0("pred_train", i)
compare_train <-
mutate(compare_train,!!varname := c(
rep(NA, FLAGS$n_timesteps + i - 1),
pred_train[i,],
rep(NA, nrow(compare_train) - FLAGS$n_timesteps * 2 - i + 1)
))
}We compute the common RSME over all sequences of predictions.
21.01495How do these predictions actually look? As a visualization of all predicted sequences would look fairly crowded, we arbitrarily decide begin factors at common intervals.
ggplot(compare_train, aes(x = index, y = worth)) + geom_line() +
geom_line(aes(y = pred_train1), coloration = "cyan") +
geom_line(aes(y = pred_train50), coloration = "purple") +
geom_line(aes(y = pred_train100), coloration = "inexperienced") +
geom_line(aes(y = pred_train150), coloration = "violet") +
geom_line(aes(y = pred_train200), coloration = "cyan") +
geom_line(aes(y = pred_train250), coloration = "purple") +
geom_line(aes(y = pred_train300), coloration = "purple") +
geom_line(aes(y = pred_train350), coloration = "inexperienced") +
geom_line(aes(y = pred_train400), coloration = "cyan") +
geom_line(aes(y = pred_train450), coloration = "purple") +
geom_line(aes(y = pred_train500), coloration = "inexperienced") +
geom_line(aes(y = pred_train550), coloration = "violet") +
geom_line(aes(y = pred_train600), coloration = "cyan") +
geom_line(aes(y = pred_train650), coloration = "purple") +
geom_line(aes(y = pred_train700), coloration = "purple") +
geom_line(aes(y = pred_train750), coloration = "inexperienced") +
ggtitle("Predictions on the coaching set")
This appears to be like fairly good. From the validation loss, we don’t fairly count on the identical from the check set, although.
Let’s see.
pred_test <- mannequin %>%
predict(X_test, batch_size = FLAGS$batch_size) %>%
.[, , 1]
# Retransform values to unique scale
pred_test <- (pred_test * scale_history + center_history) ^2
pred_test[1:10, 1:5] %>% print()
compare_test <- df %>% filter(key == "testing")
# construct a dataframe that has each precise and predicted values
for (i in 1:nrow(pred_test)) {
varname <- paste0("pred_test", i)
compare_test <-
mutate(compare_test,!!varname := c(
rep(NA, FLAGS$n_timesteps + i - 1),
pred_test[i,],
rep(NA, nrow(compare_test) - FLAGS$n_timesteps * 2 - i + 1)
))
}
compare_test %>% write_csv(str_replace(model_path, ".hdf5", ".check.csv"))
compare_test[FLAGS$n_timesteps:(FLAGS$n_timesteps + 10), c(2, 4:8)] %>% print()
coln <- colnames(compare_test)[4:ncol(compare_test)]
cols <- map(coln, quo(sym(.)))
rsme_test <-
map_dbl(cols, operate(col)
rmse(
compare_test,
reality = worth,
estimate = !!col,
na.rm = TRUE
)) %>% imply()
rsme_test31.31616ggplot(compare_test, aes(x = index, y = worth)) + geom_line() +
geom_line(aes(y = pred_test1), coloration = "cyan") +
geom_line(aes(y = pred_test50), coloration = "purple") +
geom_line(aes(y = pred_test100), coloration = "inexperienced") +
geom_line(aes(y = pred_test150), coloration = "violet") +
geom_line(aes(y = pred_test200), coloration = "cyan") +
geom_line(aes(y = pred_test250), coloration = "purple") +
geom_line(aes(y = pred_test300), coloration = "inexperienced") +
geom_line(aes(y = pred_test350), coloration = "cyan") +
geom_line(aes(y = pred_test400), coloration = "purple") +
geom_line(aes(y = pred_test450), coloration = "inexperienced") +
geom_line(aes(y = pred_test500), coloration = "cyan") +
geom_line(aes(y = pred_test550), coloration = "violet") +
ggtitle("Predictions on check set")
That’s not so good as on the coaching set, however not unhealthy both, given this time collection is kind of difficult.
Having outlined and run our mannequin on a manually chosen instance break up, let’s now revert to our general re-sampling body.
Backtesting the mannequin on all splits
To acquire predictions on all splits, we transfer the above code right into a operate and apply it to all splits.
First, right here’s the operate. It returns an inventory of two dataframes, one for the coaching and check units every, that comprise the mannequin’s predictions along with the precise values.
obtain_predictions <- operate(break up) {
df_trn <- evaluation(break up)[1:800, , drop = FALSE]
df_val <- evaluation(break up)[801:1200, , drop = FALSE]
df_tst <- evaluation(break up)
df <- bind_rows(
df_trn %>% add_column(key = "coaching"),
df_val %>% add_column(key = "validation"),
df_tst %>% add_column(key = "testing")
) %>%
as_tbl_time(index = index)
rec_obj <- recipe(worth ~ ., df) %>%
step_sqrt(worth) %>%
step_center(worth) %>%
step_scale(worth) %>%
prep()
df_processed_tbl <- bake(rec_obj, df)
center_history <- rec_obj$steps[[2]]$means["value"]
scale_history <- rec_obj$steps[[3]]$sds["value"]
FLAGS <- flags(
flag_boolean("stateful", FALSE),
flag_boolean("stack_layers", FALSE),
flag_integer("batch_size", 10),
flag_integer("n_timesteps", 12),
flag_integer("n_epochs", 100),
flag_numeric("dropout", 0.2),
flag_numeric("recurrent_dropout", 0.2),
flag_string("loss", "logcosh"),
flag_string("optimizer_type", "sgd"),
flag_integer("n_units", 128),
flag_numeric("lr", 0.003),
flag_numeric("momentum", 0.9),
flag_integer("persistence", 10)
)
n_predictions <- FLAGS$n_timesteps
n_features <- 1
optimizer <- change(FLAGS$optimizer_type,
sgd = optimizer_sgd(lr = FLAGS$lr, momentum = FLAGS$momentum))
callbacks <- checklist(
callback_early_stopping(persistence = FLAGS$persistence)
)
train_vals <- df_processed_tbl %>%
filter(key == "coaching") %>%
choose(worth) %>%
pull()
valid_vals <- df_processed_tbl %>%
filter(key == "validation") %>%
choose(worth) %>%
pull()
test_vals <- df_processed_tbl %>%
filter(key == "testing") %>%
choose(worth) %>%
pull()
train_matrix <-
build_matrix(train_vals, FLAGS$n_timesteps + n_predictions)
valid_matrix <-
build_matrix(valid_vals, FLAGS$n_timesteps + n_predictions)
test_matrix <-
build_matrix(test_vals, FLAGS$n_timesteps + n_predictions)
X_train <- train_matrix[, 1:FLAGS$n_timesteps]
y_train <-
train_matrix[, (FLAGS$n_timesteps + 1):(FLAGS$n_timesteps * 2)]
X_train <-
X_train[1:(nrow(X_train) %/% FLAGS$batch_size * FLAGS$batch_size),]
y_train <-
y_train[1:(nrow(y_train) %/% FLAGS$batch_size * FLAGS$batch_size),]
X_valid <- valid_matrix[, 1:FLAGS$n_timesteps]
y_valid <-
valid_matrix[, (FLAGS$n_timesteps + 1):(FLAGS$n_timesteps * 2)]
X_valid <-
X_valid[1:(nrow(X_valid) %/% FLAGS$batch_size * FLAGS$batch_size),]
y_valid <-
y_valid[1:(nrow(y_valid) %/% FLAGS$batch_size * FLAGS$batch_size),]
X_test <- test_matrix[, 1:FLAGS$n_timesteps]
y_test <-
test_matrix[, (FLAGS$n_timesteps + 1):(FLAGS$n_timesteps * 2)]
X_test <-
X_test[1:(nrow(X_test) %/% FLAGS$batch_size * FLAGS$batch_size),]
y_test <-
y_test[1:(nrow(y_test) %/% FLAGS$batch_size * FLAGS$batch_size),]
X_train <- reshape_X_3d(X_train)
X_valid <- reshape_X_3d(X_valid)
X_test <- reshape_X_3d(X_test)
y_train <- reshape_X_3d(y_train)
y_valid <- reshape_X_3d(y_valid)
y_test <- reshape_X_3d(y_test)
mannequin <- keras_model_sequential()
mannequin %>%
layer_lstm(
models = FLAGS$n_units,
batch_input_shape = c(FLAGS$batch_size, FLAGS$n_timesteps, n_features),
dropout = FLAGS$dropout,
recurrent_dropout = FLAGS$recurrent_dropout,
return_sequences = TRUE
) %>% time_distributed(layer_dense(models = 1))
mannequin %>%
compile(
loss = FLAGS$loss,
optimizer = optimizer,
metrics = checklist("mean_squared_error")
)
mannequin %>% match(
x = X_train,
y = y_train,
validation_data = checklist(X_valid, y_valid),
batch_size = FLAGS$batch_size,
epochs = FLAGS$n_epochs,
callbacks = callbacks
)
pred_train <- mannequin %>%
predict(X_train, batch_size = FLAGS$batch_size) %>%
.[, , 1]
# Retransform values
pred_train <- (pred_train * scale_history + center_history) ^ 2
compare_train <- df %>% filter(key == "coaching")
for (i in 1:nrow(pred_train)) {
varname <- paste0("pred_train", i)
compare_train <-
mutate(compare_train, !!varname := c(
rep(NA, FLAGS$n_timesteps + i - 1),
pred_train[i, ],
rep(NA, nrow(compare_train) - FLAGS$n_timesteps * 2 - i + 1)
))
}
pred_test <- mannequin %>%
predict(X_test, batch_size = FLAGS$batch_size) %>%
.[, , 1]
# Retransform values
pred_test <- (pred_test * scale_history + center_history) ^ 2
compare_test <- df %>% filter(key == "testing")
for (i in 1:nrow(pred_test)) {
varname <- paste0("pred_test", i)
compare_test <-
mutate(compare_test, !!varname := c(
rep(NA, FLAGS$n_timesteps + i - 1),
pred_test[i, ],
rep(NA, nrow(compare_test) - FLAGS$n_timesteps * 2 - i + 1)
))
}
checklist(practice = compare_train, check = compare_test)
}Mapping the operate over all splits yields an inventory of predictions.
all_split_preds <- rolling_origin_resamples %>%
mutate(predict = map(splits, obtain_predictions))Calculate RMSE on all splits:
calc_rmse <- operate(df) {
coln <- colnames(df)[4:ncol(df)]
cols <- map(coln, quo(sym(.)))
map_dbl(cols, operate(col)
rmse(
df,
reality = worth,
estimate = !!col,
na.rm = TRUE
)) %>% imply()
}
all_split_preds <- all_split_preds %>% unnest(predict)
all_split_preds_train <- all_split_preds[seq(1, 11, by = 2), ]
all_split_preds_test <- all_split_preds[seq(2, 12, by = 2), ]
all_split_rmses_train <- all_split_preds_train %>%
mutate(rmse = map_dbl(predict, calc_rmse)) %>%
choose(id, rmse)
all_split_rmses_test <- all_split_preds_test %>%
mutate(rmse = map_dbl(predict, calc_rmse)) %>%
choose(id, rmse)How does it look? Right here’s RMSE on the coaching set for the 6 splits.
# A tibble: 6 x 2
id rmse
<chr> <dbl>
1 Slice1 22.2
2 Slice2 20.9
3 Slice3 18.8
4 Slice4 23.5
5 Slice5 22.1
6 Slice6 21.1# A tibble: 6 x 2
id rmse
<chr> <dbl>
1 Slice1 21.6
2 Slice2 20.6
3 Slice3 21.3
4 Slice4 31.4
5 Slice5 35.2
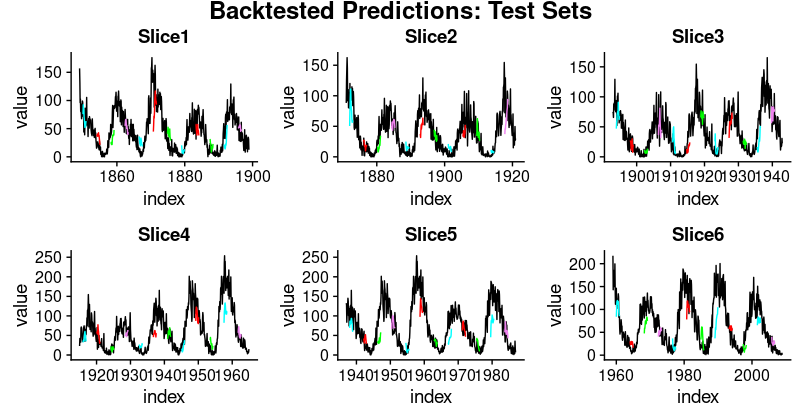
6 Slice6 31.4Taking a look at these numbers, we see one thing attention-grabbing: Generalization efficiency is significantly better for the primary three slices of the time collection than for the latter ones. This confirms our impression, acknowledged above, that there appears to be some hidden growth happening, rendering forecasting tougher.
And listed below are visualizations of the predictions on the respective coaching and check units.
First, the coaching units:
plot_train <- operate(slice, identify) {
ggplot(slice, aes(x = index, y = worth)) + geom_line() +
geom_line(aes(y = pred_train1), coloration = "cyan") +
geom_line(aes(y = pred_train50), coloration = "purple") +
geom_line(aes(y = pred_train100), coloration = "inexperienced") +
geom_line(aes(y = pred_train150), coloration = "violet") +
geom_line(aes(y = pred_train200), coloration = "cyan") +
geom_line(aes(y = pred_train250), coloration = "purple") +
geom_line(aes(y = pred_train300), coloration = "purple") +
geom_line(aes(y = pred_train350), coloration = "inexperienced") +
geom_line(aes(y = pred_train400), coloration = "cyan") +
geom_line(aes(y = pred_train450), coloration = "purple") +
geom_line(aes(y = pred_train500), coloration = "inexperienced") +
geom_line(aes(y = pred_train550), coloration = "violet") +
geom_line(aes(y = pred_train600), coloration = "cyan") +
geom_line(aes(y = pred_train650), coloration = "purple") +
geom_line(aes(y = pred_train700), coloration = "purple") +
geom_line(aes(y = pred_train750), coloration = "inexperienced") +
ggtitle(identify)
}
train_plots <- map2(all_split_preds_train$predict, all_split_preds_train$id, plot_train)
p_body_train <- plot_grid(plotlist = train_plots, ncol = 3)
p_title_train <- ggdraw() +
draw_label("Backtested Predictions: Coaching Units", measurement = 18, fontface = "daring")
plot_grid(p_title_train, p_body_train, ncol = 1, rel_heights = c(0.05, 1, 0.05))
And the check units:
plot_test <- operate(slice, identify) {
ggplot(slice, aes(x = index, y = worth)) + geom_line() +
geom_line(aes(y = pred_test1), coloration = "cyan") +
geom_line(aes(y = pred_test50), coloration = "purple") +
geom_line(aes(y = pred_test100), coloration = "inexperienced") +
geom_line(aes(y = pred_test150), coloration = "violet") +
geom_line(aes(y = pred_test200), coloration = "cyan") +
geom_line(aes(y = pred_test250), coloration = "purple") +
geom_line(aes(y = pred_test300), coloration = "inexperienced") +
geom_line(aes(y = pred_test350), coloration = "cyan") +
geom_line(aes(y = pred_test400), coloration = "purple") +
geom_line(aes(y = pred_test450), coloration = "inexperienced") +
geom_line(aes(y = pred_test500), coloration = "cyan") +
geom_line(aes(y = pred_test550), coloration = "violet") +
ggtitle(identify)
}
test_plots <- map2(all_split_preds_test$predict, all_split_preds_test$id, plot_test)
p_body_test <- plot_grid(plotlist = test_plots, ncol = 3)
p_title_test <- ggdraw() +
draw_label("Backtested Predictions: Check Units", measurement = 18, fontface = "daring")
plot_grid(p_title_test, p_body_test, ncol = 1, rel_heights = c(0.05, 1, 0.05))
This has been an extended publish, and essentially can have left lots of questions open, in the beginning: How will we acquire good settings for the hyperparameters (studying charge, variety of epochs, dropout)?
How will we select the size of the hidden state? And even, can we now have an instinct how properly LSTM will carry out on a given dataset (with its particular traits)?
We are going to sort out questions just like the above in upcoming posts.