When what just isn’t sufficient
True, typically it’s important to differentiate between completely different sorts of objects. Is {that a} automobile dashing in direction of me, through which case I’d higher leap out of the way in which? Or is it an enormous Doberman (through which case I’d in all probability do the identical)? Usually in actual life although, as a substitute of coarse-grained classification, what is required is fine-grained segmentation.
Zooming in on photos, we’re not on the lookout for a single label; as a substitute, we need to classify each pixel in line with some criterion:
-
In medication, we might need to distinguish between completely different cell varieties, or establish tumors.
-
In numerous earth sciences, satellite tv for pc knowledge are used to section terrestrial surfaces.
-
To allow use of customized backgrounds, video-conferencing software program has to have the ability to inform foreground from background.
Picture segmentation is a type of supervised studying: Some sort of floor fact is required. Right here, it is available in type of a masks – a picture, of spatial decision equivalent to that of the enter knowledge, that designates the true class for each pixel. Accordingly, classification loss is calculated pixel-wise; losses are then summed as much as yield an mixture for use in optimization.
The “canonical” structure for picture segmentation is U-Internet (round since 2015).
U-Internet
Right here is the prototypical U-Internet, as depicted within the authentic Rönneberger et al. paper (Ronneberger, Fischer, and Brox 2015).
Of this structure, quite a few variants exist. You would use completely different layer sizes, activations, methods to realize downsizing and upsizing, and extra. Nonetheless, there’s one defining attribute: the U-shape, stabilized by the “bridges” crossing over horizontally in any respect ranges.

In a nutshell, the left-hand aspect of the U resembles the convolutional architectures utilized in picture classification. It successively reduces spatial decision. On the similar time, one other dimension – the channels dimension – is used to construct up a hierarchy of options, starting from very primary to very specialised.
In contrast to in classification, nonetheless, the output ought to have the identical spatial decision because the enter. Thus, we have to upsize once more – that is taken care of by the right-hand aspect of the U. However, how are we going to reach at an excellent per-pixel classification, now that a lot spatial info has been misplaced?
That is what the “bridges” are for: At every degree, the enter to an upsampling layer is a concatenation of the earlier layer’s output – which went by the entire compression/decompression routine – and a few preserved intermediate illustration from the downsizing section. On this approach, a U-Internet structure combines consideration to element with characteristic extraction.
Mind picture segmentation
With U-Internet, area applicability is as broad because the structure is versatile. Right here, we need to detect abnormalities in mind scans. The dataset, utilized in Buda, Saha, and Mazurowski (2019), accommodates MRI photos along with manually created FLAIR abnormality segmentation masks. It’s out there on Kaggle.
Properly, the paper is accompanied by a GitHub repository. Under, we carefully comply with (although not precisely replicate) the authors’ preprocessing and knowledge augmentation code.
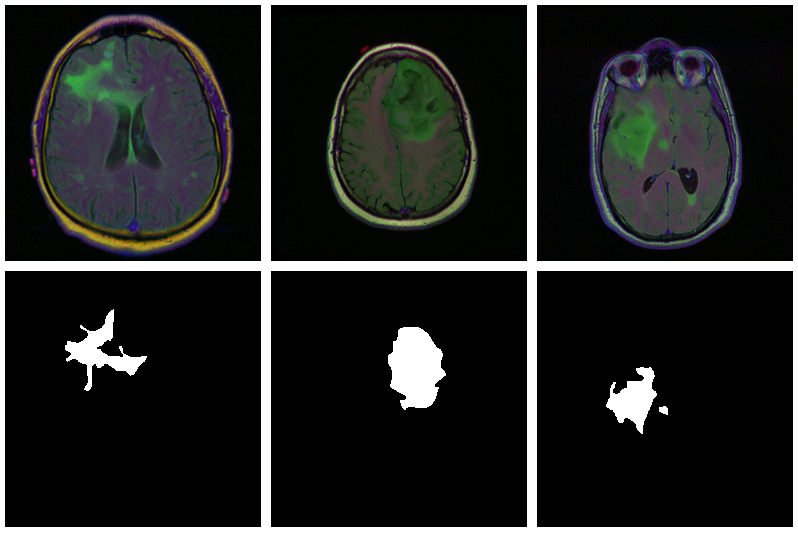
As is usually the case in medical imaging, there’s notable class imbalance within the knowledge. For each affected person, sections have been taken at a number of positions. (Variety of sections per affected person varies.) Most sections don’t exhibit any lesions; the corresponding masks are coloured black in every single place.
Listed below are three examples the place the masks do point out abnormalities:

Let’s see if we will construct a U-Internet that generates such masks for us.
Information
Earlier than you begin typing, here’s a Colaboratory pocket book to conveniently comply with alongside.
We use pins to acquire the information. Please see this introduction when you haven’t used that package deal earlier than.
The dataset just isn’t that large – it contains scans from 110 completely different sufferers – so we’ll need to do with only a coaching and a validation set. (Don’t do that in actual life, as you’ll inevitably find yourself fine-tuning on the latter.)
train_dir <- "knowledge/mri_train"
valid_dir <- "knowledge/mri_valid"
if(dir.exists(train_dir)) unlink(train_dir, recursive = TRUE, pressure = TRUE)
if(dir.exists(valid_dir)) unlink(valid_dir, recursive = TRUE, pressure = TRUE)
zip::unzip(information, exdir = "knowledge")
file.rename("knowledge/kaggle_3m", train_dir)
# it is a duplicate, once more containing kaggle_3m (evidently a packaging error on Kaggle)
# we simply take away it
unlink("knowledge/lgg-mri-segmentation", recursive = TRUE)
dir.create(valid_dir)Of these 110 sufferers, we maintain 30 for validation. Some extra file manipulations, and we’re arrange with a pleasant hierarchical construction, with train_dir and valid_dir holding their per-patient sub-directories, respectively.
valid_indices <- pattern(1:size(sufferers), 30)
sufferers <- listing.dirs(train_dir, recursive = FALSE)
for (i in valid_indices) {
dir.create(file.path(valid_dir, basename(sufferers[i])))
for (f in listing.information(sufferers[i])) {
file.rename(file.path(train_dir, basename(sufferers[i]), f), file.path(valid_dir, basename(sufferers[i]), f))
}
unlink(file.path(train_dir, basename(sufferers[i])), recursive = TRUE)
}We now want a dataset that is aware of what to do with these information.
Dataset
Like each torch dataset, this one has initialize() and .getitem() strategies. initialize() creates a list of scan and masks file names, for use by .getitem() when it truly reads these information. In distinction to what we’ve seen in earlier posts, although , .getitem() doesn’t merely return input-target pairs so as. As a substitute, every time the parameter random_sampling is true, it is going to carry out weighted sampling, preferring gadgets with sizable lesions. This feature can be used for the coaching set, to counter the category imbalance talked about above.
The opposite approach coaching and validation units will differ is use of knowledge augmentation. Coaching photos/masks could also be flipped, re-sized, and rotated; possibilities and quantities are configurable.
An occasion of brainseg_dataset encapsulates all this performance:
brainseg_dataset <- dataset(
identify = "brainseg_dataset",
initialize = operate(img_dir,
augmentation_params = NULL,
random_sampling = FALSE) {
self$photos <- tibble(
img = grep(
listing.information(
img_dir,
full.names = TRUE,
sample = "tif",
recursive = TRUE
),
sample = 'masks',
invert = TRUE,
worth = TRUE
),
masks = grep(
listing.information(
img_dir,
full.names = TRUE,
sample = "tif",
recursive = TRUE
),
sample = 'masks',
worth = TRUE
)
)
self$slice_weights <- self$calc_slice_weights(self$photos$masks)
self$augmentation_params <- augmentation_params
self$random_sampling <- random_sampling
},
.getitem = operate(i) {
index <-
if (self$random_sampling == TRUE)
pattern(1:self$.size(), 1, prob = self$slice_weights)
else
i
img <- self$photos$img[index] %>%
image_read() %>%
transform_to_tensor()
masks <- self$photos$masks[index] %>%
image_read() %>%
transform_to_tensor() %>%
transform_rgb_to_grayscale() %>%
torch_unsqueeze(1)
img <- self$min_max_scale(img)
if (!is.null(self$augmentation_params)) {
scale_param <- self$augmentation_params[1]
c(img, masks) %<-% self$resize(img, masks, scale_param)
rot_param <- self$augmentation_params[2]
c(img, masks) %<-% self$rotate(img, masks, rot_param)
flip_param <- self$augmentation_params[3]
c(img, masks) %<-% self$flip(img, masks, flip_param)
}
listing(img = img, masks = masks)
},
.size = operate() {
nrow(self$photos)
},
calc_slice_weights = operate(masks) {
weights <- map_dbl(masks, operate(m) {
img <-
as.integer(magick::image_data(image_read(m), channels = "grey"))
sum(img / 255)
})
sum_weights <- sum(weights)
num_weights <- size(weights)
weights <- weights %>% map_dbl(operate(w) {
w <- (w + sum_weights * 0.1 / num_weights) / (sum_weights * 1.1)
})
weights
},
min_max_scale = operate(x) {
min = x$min()$merchandise()
max = x$max()$merchandise()
x$clamp_(min = min, max = max)
x$add_(-min)$div_(max - min + 1e-5)
x
},
resize = operate(img, masks, scale_param) {
img_size <- dim(img)[2]
rnd_scale <- runif(1, 1 - scale_param, 1 + scale_param)
img <- transform_resize(img, measurement = rnd_scale * img_size)
masks <- transform_resize(masks, measurement = rnd_scale * img_size)
diff <- dim(img)[2] - img_size
if (diff > 0) {
high <- ceiling(diff / 2)
left <- ceiling(diff / 2)
img <- transform_crop(img, high, left, img_size, img_size)
masks <- transform_crop(masks, high, left, img_size, img_size)
} else {
img <- transform_pad(img,
padding = -c(
ceiling(diff / 2),
ground(diff / 2),
ceiling(diff / 2),
ground(diff / 2)
))
masks <- transform_pad(masks, padding = -c(
ceiling(diff / 2),
ground(diff /
2),
ceiling(diff /
2),
ground(diff /
2)
))
}
listing(img, masks)
},
rotate = operate(img, masks, rot_param) {
rnd_rot <- runif(1, 1 - rot_param, 1 + rot_param)
img <- transform_rotate(img, angle = rnd_rot)
masks <- transform_rotate(masks, angle = rnd_rot)
listing(img, masks)
},
flip = operate(img, masks, flip_param) {
rnd_flip <- runif(1)
if (rnd_flip > flip_param) {
img <- transform_hflip(img)
masks <- transform_hflip(masks)
}
listing(img, masks)
}
)After instantiation, we see we’ve got 2977 coaching pairs and 952 validation pairs, respectively:
As a correctness examine, let’s plot a picture and related masks:

With torch, it’s easy to examine what occurs if you change augmentation-related parameters. We simply decide a pair from the validation set, which has not had any augmentation utilized as but, and name valid_ds$<augmentation_func()> instantly. Only for enjoyable, let’s use extra “excessive” parameters right here than we do in precise coaching. (Precise coaching makes use of the settings from Mateusz’ GitHub repository, which we assume have been fastidiously chosen for optimum efficiency.)
img_and_mask <- valid_ds[77]
img <- img_and_mask[[1]]
masks <- img_and_mask[[2]]
imgs <- map (1:24, operate(i) {
# scale issue; train_ds actually makes use of 0.05
c(img, masks) %<-% valid_ds$resize(img, masks, 0.2)
c(img, masks) %<-% valid_ds$flip(img, masks, 0.5)
# rotation angle; train_ds actually makes use of 15
c(img, masks) %<-% valid_ds$rotate(img, masks, 90)
img %>%
transform_rgb_to_grayscale() %>%
as.array() %>%
as_tibble() %>%
rowid_to_column(var = "Y") %>%
collect(key = "X", worth = "worth", -Y) %>%
mutate(X = as.numeric(gsub("V", "", X))) %>%
ggplot(aes(X, Y, fill = worth)) +
geom_raster() +
theme_void() +
theme(legend.place = "none") +
theme(side.ratio = 1)
})
plot_grid(plotlist = imgs, nrow = 4)
Now we nonetheless want the information loaders, after which, nothing retains us from continuing to the following large process: constructing the mannequin.
batch_size <- 4
train_dl <- dataloader(train_ds, batch_size)
valid_dl <- dataloader(valid_ds, batch_size)Mannequin
Our mannequin properly illustrates the sort of modular code that comes “naturally” with torch. We method issues top-down, beginning with the U-Internet container itself.
unet takes care of the worldwide composition – how far “down” can we go, shrinking the picture whereas incrementing the variety of filters, after which how can we go “up” once more?
Importantly, additionally it is within the system’s reminiscence. In ahead(), it retains observe of layer outputs seen going “down,” to be added again in going “up.”
unet <- nn_module(
"unet",
initialize = operate(channels_in = 3,
n_classes = 1,
depth = 5,
n_filters = 6) {
self$down_path <- nn_module_list()
prev_channels <- channels_in
for (i in 1:depth) {
self$down_path$append(down_block(prev_channels, 2 ^ (n_filters + i - 1)))
prev_channels <- 2 ^ (n_filters + i -1)
}
self$up_path <- nn_module_list()
for (i in ((depth - 1):1)) {
self$up_path$append(up_block(prev_channels, 2 ^ (n_filters + i - 1)))
prev_channels <- 2 ^ (n_filters + i - 1)
}
self$final = nn_conv2d(prev_channels, n_classes, kernel_size = 1)
},
ahead = operate(x) {
blocks <- listing()
for (i in 1:size(self$down_path)) {
x <- self$down_path[[i]](x)
if (i != size(self$down_path)) {
blocks <- c(blocks, x)
x <- nnf_max_pool2d(x, 2)
}
}
for (i in 1:size(self$up_path)) {
x <- self$up_path[[i]](x, blocks[[length(blocks) - i + 1]]$to(system = system))
}
torch_sigmoid(self$final(x))
}
)unet delegates to 2 containers slightly below it within the hierarchy: down_block and up_block. Whereas down_block is “simply” there for aesthetic causes (it instantly delegates to its personal workhorse, conv_block), in up_block we see the U-Internet “bridges” in motion.
down_block <- nn_module(
"down_block",
initialize = operate(in_size, out_size) {
self$conv_block <- conv_block(in_size, out_size)
},
ahead = operate(x) {
self$conv_block(x)
}
)
up_block <- nn_module(
"up_block",
initialize = operate(in_size, out_size) {
self$up = nn_conv_transpose2d(in_size,
out_size,
kernel_size = 2,
stride = 2)
self$conv_block = conv_block(in_size, out_size)
},
ahead = operate(x, bridge) {
up <- self$up(x)
torch_cat(listing(up, bridge), 2) %>%
self$conv_block()
}
)Lastly, a conv_block is a sequential construction containing convolutional, ReLU, and dropout layers.
conv_block <- nn_module(
"conv_block",
initialize = operate(in_size, out_size) {
self$conv_block <- nn_sequential(
nn_conv2d(in_size, out_size, kernel_size = 3, padding = 1),
nn_relu(),
nn_dropout(0.6),
nn_conv2d(out_size, out_size, kernel_size = 3, padding = 1),
nn_relu()
)
},
ahead = operate(x){
self$conv_block(x)
}
)Now instantiate the mannequin, and probably, transfer it to the GPU:
system <- torch_device(if(cuda_is_available()) "cuda" else "cpu")
mannequin <- unet(depth = 5)$to(system = system)Optimization
We prepare our mannequin with a mixture of cross entropy and cube loss.
The latter, although not shipped with torch, could also be applied manually:
calc_dice_loss <- operate(y_pred, y_true) {
clean <- 1
y_pred <- y_pred$view(-1)
y_true <- y_true$view(-1)
intersection <- (y_pred * y_true)$sum()
1 - ((2 * intersection + clean) / (y_pred$sum() + y_true$sum() + clean))
}
dice_weight <- 0.3Optimization makes use of stochastic gradient descent (SGD), along with the one-cycle studying fee scheduler launched within the context of picture classification with torch.
optimizer <- optim_sgd(mannequin$parameters, lr = 0.1, momentum = 0.9)
num_epochs <- 20
scheduler <- lr_one_cycle(
optimizer,
max_lr = 0.1,
steps_per_epoch = size(train_dl),
epochs = num_epochs
)Coaching
The coaching loop then follows the standard scheme. One factor to notice: Each epoch, we save the mannequin (utilizing torch_save()), so we will later decide the most effective one, ought to efficiency have degraded thereafter.
train_batch <- operate(b) {
optimizer$zero_grad()
output <- mannequin(b[[1]]$to(system = system))
goal <- b[[2]]$to(system = system)
bce_loss <- nnf_binary_cross_entropy(output, goal)
dice_loss <- calc_dice_loss(output, goal)
loss <- dice_weight * dice_loss + (1 - dice_weight) * bce_loss
loss$backward()
optimizer$step()
scheduler$step()
listing(bce_loss$merchandise(), dice_loss$merchandise(), loss$merchandise())
}
valid_batch <- operate(b) {
output <- mannequin(b[[1]]$to(system = system))
goal <- b[[2]]$to(system = system)
bce_loss <- nnf_binary_cross_entropy(output, goal)
dice_loss <- calc_dice_loss(output, goal)
loss <- dice_weight * dice_loss + (1 - dice_weight) * bce_loss
listing(bce_loss$merchandise(), dice_loss$merchandise(), loss$merchandise())
}
for (epoch in 1:num_epochs) {
mannequin$prepare()
train_bce <- c()
train_dice <- c()
train_loss <- c()
coro::loop(for (b in train_dl) {
c(bce_loss, dice_loss, loss) %<-% train_batch(b)
train_bce <- c(train_bce, bce_loss)
train_dice <- c(train_dice, dice_loss)
train_loss <- c(train_loss, loss)
})
torch_save(mannequin, paste0("model_", epoch, ".pt"))
cat(sprintf("nEpoch %d, coaching: loss:%3f, bce: %3f, cube: %3fn",
epoch, imply(train_loss), imply(train_bce), imply(train_dice)))
mannequin$eval()
valid_bce <- c()
valid_dice <- c()
valid_loss <- c()
i <- 0
coro::loop(for (b in tvalid_dl) {
i <<- i + 1
c(bce_loss, dice_loss, loss) %<-% valid_batch(b)
valid_bce <- c(valid_bce, bce_loss)
valid_dice <- c(valid_dice, dice_loss)
valid_loss <- c(valid_loss, loss)
})
cat(sprintf("nEpoch %d, validation: loss:%3f, bce: %3f, cube: %3fn",
epoch, imply(valid_loss), imply(valid_bce), imply(valid_dice)))
}Epoch 1, coaching: loss:0.304232, bce: 0.148578, cube: 0.667423
Epoch 1, validation: loss:0.333961, bce: 0.127171, cube: 0.816471
Epoch 2, coaching: loss:0.194665, bce: 0.101973, cube: 0.410945
Epoch 2, validation: loss:0.341121, bce: 0.117465, cube: 0.862983
[...]
Epoch 19, coaching: loss:0.073863, bce: 0.038559, cube: 0.156236
Epoch 19, validation: loss:0.302878, bce: 0.109721, cube: 0.753577
Epoch 20, coaching: loss:0.070621, bce: 0.036578, cube: 0.150055
Epoch 20, validation: loss:0.295852, bce: 0.101750, cube: 0.748757Analysis
On this run, it’s the ultimate mannequin that performs greatest on the validation set. Nonetheless, we’d like to indicate easy methods to load a saved mannequin, utilizing torch_load() .
As soon as loaded, put the mannequin into eval mode:
saved_model <- torch_load("model_20.pt")
mannequin <- saved_model
mannequin$eval()Now, since we don’t have a separate check set, we already know the typical out-of-sample metrics; however ultimately, what we care about are the generated masks. Let’s view some, displaying floor fact and MRI scans for comparability.
# with out random sampling, we might primarily see lesion-free patches
eval_ds <- brainseg_dataset(valid_dir, augmentation_params = NULL, random_sampling = TRUE)
eval_dl <- dataloader(eval_ds, batch_size = 8)
batch <- eval_dl %>% dataloader_make_iter() %>% dataloader_next()
par(mfcol = c(3, 8), mar = c(0, 1, 0, 1))
for (i in 1:8) {
img <- batch[[1]][i, .., drop = FALSE]
inferred_mask <- mannequin(img$to(system = system))
true_mask <- batch[[2]][i, .., drop = FALSE]$to(system = system)
bce <- nnf_binary_cross_entropy(inferred_mask, true_mask)$to(system = "cpu") %>%
as.numeric()
dc <- calc_dice_loss(inferred_mask, true_mask)$to(system = "cpu") %>% as.numeric()
cat(sprintf("nSample %d, bce: %3f, cube: %3fn", i, bce, dc))
inferred_mask <- inferred_mask$to(system = "cpu") %>% as.array() %>% .[1, 1, , ]
inferred_mask <- ifelse(inferred_mask > 0.5, 1, 0)
img[1, 1, ,] %>% as.array() %>% as.raster() %>% plot()
true_mask$to(system = "cpu")[1, 1, ,] %>% as.array() %>% as.raster() %>% plot()
inferred_mask %>% as.raster() %>% plot()
}We additionally print the person cross entropy and cube losses; relating these to the generated masks may yield helpful info for mannequin tuning.
Pattern 1, bce: 0.088406, cube: 0.387786}
Pattern 2, bce: 0.026839, cube: 0.205724
Pattern 3, bce: 0.042575, cube: 0.187884
Pattern 4, bce: 0.094989, cube: 0.273895
Pattern 5, bce: 0.026839, cube: 0.205724
Pattern 6, bce: 0.020917, cube: 0.139484
Pattern 7, bce: 0.094989, cube: 0.273895
Pattern 8, bce: 2.310956, cube: 0.999824
Whereas removed from excellent, most of those masks aren’t that dangerous – a pleasant consequence given the small dataset!
Wrapup
This has been our most complicated torch put up to date; nonetheless, we hope you’ve discovered the time effectively spent. For one, amongst functions of deep studying, medical picture segmentation stands out as extremely societally helpful. Secondly, U-Internet-like architectures are employed in lots of different areas. And eventually, we as soon as extra noticed torch’s flexibility and intuitive habits in motion.
Thanks for studying!