When quantum computer systems have been first proposed, they have been hoped to be a method to higher perceive the quantum world. With a so-called “quantum simulator,” one may engineer a quantum pc to research how numerous quantum phenomena come up, together with these which are intractable to simulate with a classical pc.
However making a helpful quantum simulator has been a problem. Till now, quantum simulations with superconducting qubits have predominantly been used to confirm pre-existing theoretical predictions and have hardly ever explored or found new phenomena. Only some experiments with trapped ions or chilly atoms have revealed new insights. Superconducting qubits, although they’re one of many principal candidates for common quantum computing and have demonstrated computational capabilities past classical attain, have to this point not delivered on their potential for discovery.
In “Formation of Sturdy Certain States of Interacting Photons”, revealed in Nature, we describe a beforehand unpredicted phenomenon first found via experimental investigation. First, we current the experimental affirmation of the theoretical prediction of the existence of a composite particle of interacting photons, or a sure state, utilizing the Google Sycamore quantum processor. Second, whereas learning this technique, we found that although one would possibly guess the sure states to be fragile, they continue to be strong to perturbations that we anticipated to have in any other case destroyed them. Not solely does this open the opportunity of designing techniques that leverage interactions between photons, it additionally marks a step ahead in using superconducting quantum processors to make new scientific discoveries by simulating non-equilibrium quantum dynamics.
Overview
Photons, or quanta of electromagnetic radiation like mild and microwaves, usually don’t work together. For instance, two intersecting flashlight beams will cross via each other undisturbed. In lots of purposes, like telecommunications, the weak interactions of photons is a helpful characteristic. For different purposes, resembling computer systems primarily based on mild, the dearth of interactions between photons is a shortcoming.
In a quantum processor, the qubits host microwave photons, which could be made to work together via two-qubit operations. This permits us to simulate the XXZ mannequin, which describes the habits of interacting photons. Importantly, this is likely one of the few examples of integrable fashions, i.e., one with a excessive diploma of symmetry, which significantly reduces its complexity. After we implement the XXZ mannequin on the Sycamore processor, we observe one thing hanging: the interactions power the photons into bundles often called sure states.
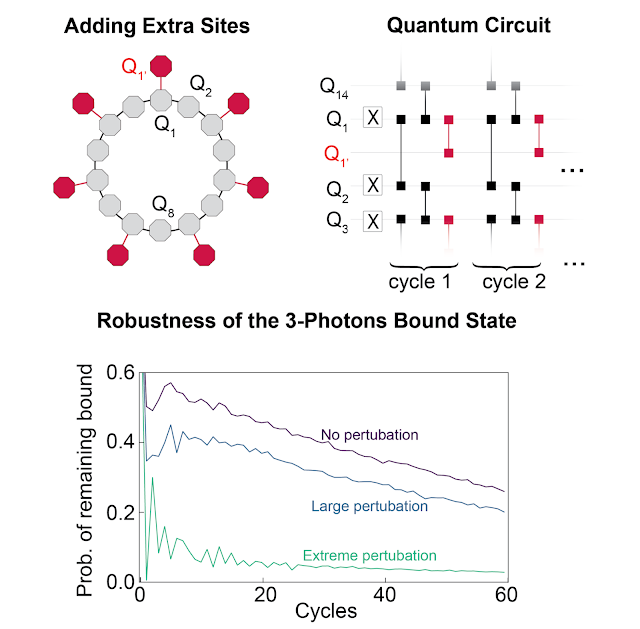
Utilizing this well-understood mannequin as a place to begin, we then push the examine right into a less-understood regime. We break the excessive degree of symmetries displayed within the XXZ mannequin by including further websites that may be occupied by the photons, making the system not integrable. Whereas this nonintegrable regime is anticipated to exhibit chaotic habits the place sure states dissolve into their traditional, solitary selves, we as a substitute discover that they survive!
Certain Photons
To engineer a system that may help the formation of sure states, we examine a hoop of superconducting qubits that host microwave photons. If a photon is current, the worth of the qubit is “1”, and if not, the worth is “0”. By way of the so-called “fSim” quantum gate, we join neighboring websites, permitting the photons to hop round and work together with different photons on the nearest-neighboring websites.
 |
| Superconducting qubits could be occupied or unoccupied with microwave photons. The “fSim” gate operation permits photons to hop and work together with one another. The corresponding unitary evolution has a hopping time period between two websites (orange) and an interplay time period equivalent to an added section when two adjoining websites are occupied by a photon. |
 |
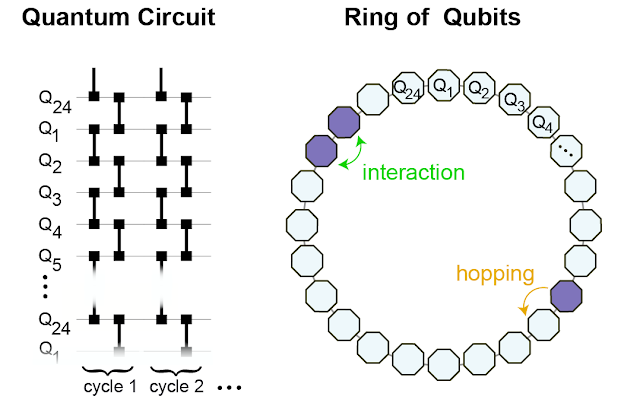| We implement the fSim gate between neighboring qubits (left) to successfully kind a hoop of 24 interconnected qubits on which we simulate the habits of the interacting photons (proper). |
The interactions between the photons have an effect on their so-called “section.” This section retains observe of the oscillation of the photon’s wavefunction. When the photons are non-interacting, their section accumulation is slightly uninteresting. Like a well-rehearsed choir, they’re all in sync with each other. On this case, a photon that was initially subsequent to a different photon can hop away from its neighbor with out getting out of sync. Simply as each individual within the choir contributes to the music, each potential path the photon can take contributes to the photon’s total wavefunction. A gaggle of photons initially clustered on neighboring websites will evolve right into a superposition of all potential paths every photon may need taken.
When photons work together with their neighbors, that is not the case. If one photon hops away from its neighbor, its charge of section accumulation modifications, turning into out of sync with its neighbors. All paths during which the photons cut up aside overlap, resulting in harmful interference. It could be like every choir member singing at their very own tempo — the music itself will get washed out, turning into not possible to discern via the din of the person singers. Amongst all of the potential configuration paths, the one potential state of affairs that survives is the configuration during which all photons stay clustered collectively in a sure state. For this reason interplay can improve and result in the formation of a sure state: by suppressing all different potentialities during which photons usually are not sure collectively.
 |
| Left: Evolution of interacting photons forming a sure state. Proper: Time goes from left to proper, every path represents one of many paths that may break the 2-photon bonded state. Attributable to interactions, these paths intrude destructively, stopping the photons from splitting aside. |
 |
| Occupation likelihood versus gate cycle, or discrete time step, for n-photon sure states. We put together sure states of various sizes and watch them evolve. We observe that almost all of the photons (darker colours) stay sure collectively. |
In our processor, we begin by placing two to 5 photons on adjoining websites (i.e., initializing two to 5 adjoining qubits in “1”, and the remaining qubits in “0”), after which examine how they propagate. First, we discover that within the theoretically predicted parameter regime, they continue to be caught collectively. Subsequent, we discover that the bigger sure states transfer extra slowly across the ring, in line with the truth that they’re “heavier”. This may be seen within the plot above the place the lattice websites closest to Website 12, the preliminary place of the photons, stay darker than the others with rising variety of photons (nph) within the sure state, indicating that with extra photons sure collectively there’s much less propagation across the ring.
Certain States Behave Like Single Composite Particles
To extra rigorously present that the sure states certainly behave as single particles with well-defined bodily properties, we devise a way to measure how the power of the particles modifications with momentum, i.e., the energy-momentum dispersion relation.
To measure the power of the sure state, we use the truth that the power distinction between two states determines how briskly their relative section grows with time. Therefore, we put together the sure state in a superposition with the state that has no photons, and measure their section distinction as a operate of time and area. Then, to transform the results of this measurement to a dispersion relation, we make the most of a Fourier rework, which interprets place and time into momentum and power, respectively. We’re left with the acquainted energy-momentum relationship of excitations in a lattice.
 |
| Spectroscopy of sure states. We evaluate the section accumulation of an n-photon sure state with that of the vacuum (no photons) as a operate of lattice web site and time. A 2D Fourier rework yields the dispersion relation of the bound-state quasiparticle. |
Breaking Integrability
The above system is “integrable,” that means that it has a enough variety of conserved portions that its dynamics are constrained to a small a part of the accessible computational area. In such integrable regimes, the looks of sure states isn’t that shocking. In truth, sure states in comparable techniques have been predicted in 2012, then noticed in 2013. Nevertheless, these sure states are fragile and their existence is normally thought to derive from integrability. For extra complicated techniques, there’s much less symmetry and integrability is shortly misplaced. Our preliminary concept was to probe how these sure states disappear as we break integrability to higher perceive their rigidity.
To interrupt integrability, we modify which qubits are related with fSim gates. We add qubits in order that at alternating websites, along with hopping to every of its two nearest-neighboring websites, a photon may also hop to a 3rd web site oriented radially outward from the ring.
Whereas a sure state is constrained to a really small a part of section area, we anticipated that the chaotic habits related to integrability breaking would enable the system to discover the section area extra freely. This may trigger the sure states to interrupt aside. We discover that this isn’t the case. Even when the integrability breaking is so sturdy that the photons are equally more likely to hop to the third web site as they’re to hop to both of the 2 adjoining ring websites, the sure state stays intact, as much as the decoherence impact that makes them slowly decay (see paper for particulars).
 |
| Prime: New geometry to interrupt integrability. Alternating websites are related to a 3rd web site oriented radially outward. This will increase the complexity of the system, and permits for probably chaotic habits. Backside: Regardless of this added complexity pushing the system past integrability, we discover that the 3-photon sure state stays secure even for a comparatively giant perturbation. The likelihood of remaining sure decreases slowly because of decoherence (see paper). |
Conclusion
We don’t but have a satisfying clarification for this surprising resilience. We speculate that it might be associated to a phenomenon known as prethermalization, the place incommensurate power scales within the system can stop a system from reaching thermal equilibrium as shortly because it in any other case would. We consider additional investigations will hopefully result in new insights into many-body quantum physics, together with the interaction of prethermalization and integrability.
Acknowledgements
We want to thank our Quantum Science Communicator Katherine McCormick for her assist penning this weblog put up.
