Vertical assemblies of twisted or lattice-mismatched heterobilayers of two-dimensionaltransition steel dichalcogenides (TMDs) with moiré-modulated interlayer coupling give rise to correlated Hubbard-model physics1—exhibiting signatures of collective phases in each transport2,3,4,5 and optical experiments6,7,8,9. Periodic moiré interference patterns have profound results on the digital band construction attributable to formation of flat mini-bands that improve many-body correlations, and induce emergent magnetism6, correlated insulating states2,3,4,7,8,9 or Wigner crystals7. Moiré results additionally lead to wealthy optical signatures of intralayer10 and interlayer11,12,13,14 excitons which can be shaped by Coulomb points of interest amongst layer-locked and -separated electrons and holes, with angle-controlled exciton valley coherence and dynamics15,16, optical nonlinearities17 or correlated excitonic insulating states18.
Regardless of the in depth optical research of moiré results in TMD heterobilayers akin to MoSe2–WSe2 (ref. 19), a consolidated image of the wealthy experimental options stays elusive20. The experimental outcomes for the height energies of the interlayer exciton photoluminescence (PL)21,22, g-factor11,22 and diploma of polarization11,12 are inconsistent, and the PL spectra can differ considerably from spot to identify even in the identical pattern23. The range of fashions invoked to clarify the plethora of experimental signatures shouldn’t be inherent to the speculation of moiré excitons24,25,26 however is as a substitute associated to variations in precise samples. For TMD bilayers with small twist angles, particularly, canonical moiré superlattices are recognized to rework into periodic domains of distinct atomic registries in triangular or hexagonal tiling27,28,29,30,31,32,33, as dictated by the competitors between the intralayer pressure and interlayer adhesion energies34,35,36. Correlative research of reconstruction and exciton options are to date restricted to twisted homobilayers28,29, offering solely oblique perception into exciton landscapes of mesoscopically reconstructed moiré heterostructures.
Canonical and periodically reconstructed moiré heterostructures
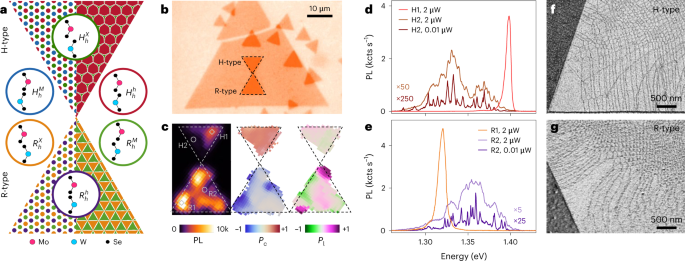
Superb moiré heterostructures emerge in vertical heterobilayer (HBL) assemblies of distinct TMD monolayers with out an inversion centre, and distinguish between parallel and antiparallel alignments close to 0° and 180° twist angles of R- and H-stackings. As a result of lattice mismatch of the monolayer constituents, each the R- and H-type heterostacks type moiré patterns with superlattice constants of ~100 nm in aligned MoSe2–WSe2 HBLs, which reduces asymptotically to the monolayer lattice fixed with growing twist away from the high-symmetry configurations. Following lateral translation by a moiré supercell, every stacking modulates by factors of extremely symmetric atomic registries (({H}_{h}^{h}), ({H}_{h}^{M}), ({H}_{h}^{X}) and ({R}_{h}^{h}), ({R}_{h}^{M}), ({R}_{h}^{X})), that are proven schematically within the colored circles of Fig. 1a for a heterostack of high MoSe2 and backside WSe2 monolayers.
a, Schematics of H- and R-type heterostacks with best moiré (left) and periodically reconstructed (proper) patterns. The colored areas signify high-symmetry atomic registries, as illustrated within the respective circles. b, Optical micrograph of pattern 1 with H- and R-stacks (delimited by dashed traces) of CVD-grown MoSe2 monolayers (small triangles) on a big WSe2 monolayer (giant triangle). c, Interlayer exciton PL map (left) with chosen vibrant (H1, R1) and darkish (H2, R2) spots indicated by diamonds and circles, respectively, in addition to Pc (center) and Pl (proper) maps for the H and R-stacks in b. d,e, Photoluminescence spectra on the vibrant and darkish spots marked in c. At an excitation energy of two μW, the H1 and R1 spectra are consultant for areas with a single vibrant peak, whereas the H2 and R2 spectra (scaled by 50 and 5, respectively) are traits of darkish areas with broad and structured PL, which evolves into slender peaks at a low excitation energy of 0.01 μW (scaled by 250 and 25, respectively). All spectroscopy information had been recorded on pattern 1. f,g, Scanning electron micrographs of H- (f) and R- (g) heterostacks recorded with secondary electron imaging.
For inflexible lattices, the ensuing moiré sample is proven on the left facet of the H (high) and R (backside) triangles (Fig. 1a). The positions of high-symmetry registries with an identical areas are represented by their respective colors, spanning a periodic lattice of laterally alternating registries with gradual interconversion in response to the geometrical interference situation. Within the presence of native lattice deformation, nonetheless, the best moiré sample transforms into periodically reconstructed patterns, that are proven on the precise facet of the triangles. Pushed by competitors between intralayer pressure and interlayer adhesion power, energetically favoured registries increase on the expense of unfavourable ones into periodic domains with areas inversely proportional to the squared twist angle θ2. Theoretical and experimental outcomes27,34 point out for H-type heterostacks that solely ({H}_{h}^{h}) stacking prevails in hexagonal domains after reconstruction, whereas in R-type heterostacks, ({R}_{h}^{X}) and ({R}_{h}^{M}) consolidate into tessellated triangular domains as two equally optimum registries.
The best and reconstructed moiré panorama situations of Fig. 1a can in precept be discerned by optical spectroscopy, regardless of the length-scale mismatch between the optical spot dimension (on the order of a micrometre) and the area dimension (dimensions effectively beneath 100 nm). Through the use of the distinct PL traits of interlayer excitons in atomic registries of MoSe2–WSe2 HBLs listed in Desk 1, the observer might infer the contribution from every area current within the optical spot. By advantage of distinctive spin-valley configurations, stacking symmetries and associated levels of interlayer coupling, R- and H-type interlayer excitons exhibit distinct transition energies25,26,36,37,38, oscillator strengths37,38 and dipolar choice guidelines25,26,39 which can be accessible by way of optical spectroscopy. Furthermore, magneto-luminescence experiments permit the task of interlayer exciton PL to the domains of particular registries utilizing first-principles calculations of exciton Landé g-factors38,40,41 and experimental values. This conceptual readability, nonetheless, is contrasted by the puzzling range of moiré exciton signatures in MoSe2–WSe2 HBLs.
Mesoscopic reconstruction in experiment and principle
On this work we fabricated HBL samples from MoSe2 and WSe2 monolayers exfoliated from native crystals or synthesized by chemical vapour deposition (CVD) (see the Strategies for particulars). For the pattern in Fig. 1b primarily based on CVD-grown monolayers, we positioned single-crystal MoSe2 triangles on high of a big WSe2 triangular monolayer by normal dry-transfer. The ensuing HBL triangles with small-twist-angle H- and R-stackings are delimited by dashed traces within the optical micrograph of Fig. 1b. The entire HBLs had been encapsulated in hexagonal boron nitride (hBN) to entry slender exciton linewidths in cryogenic spectroscopy42.
Determine 1c reveals the PL traits within the spectral bandwidth of interlayer excitons. The laterally prolonged maps recorded at 3.2 Okay present the built-in PL depth and the levels of its round (Pc) and linear (Pl) polarizations43. The PL map reveals sizable depth variations throughout each stacks, with a lot brighter emission within the R-stack. These variations are accompanied by modifications within the spectral traits, proven representatively in Fig. 1d,e. Within the upper-right and lower-left vibrant corners of the H- and R-type triangles (H1 and R1, respectively), the corresponding PL spectra function just one peak at 1.40 and 1.33 eV, with the best levels of round polarization and reverse indicators within the Pc map of Fig. 1c. These signatures collectively recommend that each stacks function areas on the size of the optical spot which can be completely dominated by the respective triplet and singlet interlayer excitons of the ({H}_{h}^{h}) and ({R}_{h}^{X}) registries. Given the finite twist angle in our pattern, the absence of PL contributions from all different registries is putting.
The signatures of vibrant spots are contrasted on positions with low PL (labels H2 and R2), and are proven as brown and purple spectra in Fig. 1d,e. On the expense of single-peak spectra, the PL is structured and spectrally dispersed over 100 meV on the low- and high-energy sides of the solitary peaks of the triplet ({H}_{h}^{h}) and singlet ({R}_{h}^{X}) interlayer excitons, respectively. On darkish spots and underneath an identical excitation situations, the built-in PL is often a lot decrease (observe the scaling by 50 and 5 for H- and R-type spectra, respectively), and Pc is lowered in its absolute worth, though preserved in signal. These options of moiré results12,23,38 evolve right into a collection of spectrally slender peaks at lowered excitation powers, signifying interlayer exciton localization in moiré quantum dots11,23.
Along with the co-existence of contrasting options in a single pattern, confusion arises from the remark of a finite diploma of linear polarization with variations throughout the Pl map of Fig. 1c. In response to Desk 1, the dipolar choice guidelines of interlayer excitons dictate valley contrasting circularly polarized out-of-plane and in-pane z-polarized transitions25,26,39. Whereas the previous represent constructive and unfavorable Pc within the maps of the H- and R-type stacking (Fig. 1c), the latter ought to exhibit neither round nor linear levels of polarization when probed in back-scattering configuration38. In contrast, the map in Fig. 1c reveals areas with excessive Pl (observe the upper- and lower-left corners of the R-type triangle), harking back to quantum wire results as in uniaxially strained moiré landscapes44 or HBL samples with transfer-induced layer corrugation45.
The entire above options manifest persistently throughout the samples of our research (see Supplementary Notes 1 and 3 for different samples). The important thing to the understanding of such variations within the optical options on one pattern is offered by mesoscopic reconstruction, which we visualize with secondary electron imaging in scanning electron microscopy (SEM)29. The pictures of H- and R-heterostacks close to the triangle edges with stacking-sensitive distinction (Fig. 1f,g and Supplementary Observe 1) present proof for the formation of enormous domains of 1 atomic registry separated by skinny traces of area partitions. The area networks noticed in several samples exhibit frequent patterns on the mesoscopic scale: prolonged 2D domains at HBL suggestions and edges are surrounded by elongated 1D stripes that merge within the pattern core right into a community of finely structured domains with dimensions effectively beneath 100 nm, forming quasi 0D arrays.
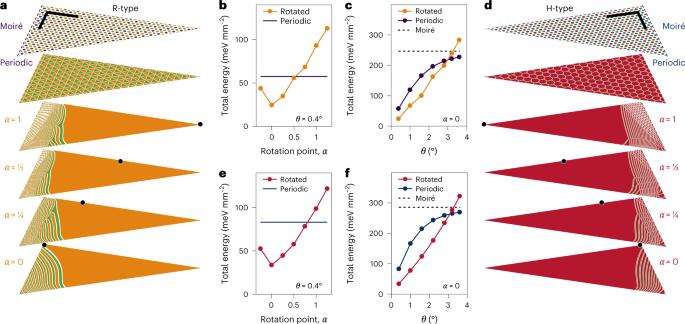
Mesoscopic reconstruction is pushed by the interaction of intralayer pressure and interlayer adhesion power. Current theoretical work34,35,36 identified that moiré lattices of marginally twisted bilayers calm down on the nanoscale into periodic domains by rearranging lattice atoms in response to a vectorial 2D displacement subject that overcompensates for the related pressure value with the acquire in interlayer adhesion. To supply instinct for area formation on scales from a couple of to a couple hundred nanometres, we undertake the theoretical mannequin of lattice reconstruction35 and account for finite dimension results and singular level rotations that may develop to large-area 2D domains of optimum stacking. Briefly, we mannequin the tip of a HBL with small twist angles through the use of an equilateral triangle, with its micrometre-sized base connecting to the remainder of the triangle with best moiré periodicity (see Supplementary Observe 2 for particulars). On the road bisecting the triangular tip into two equal halves, we place a degree of zero-twist deformation to create an preliminary lattice-displacement subject, which is modified in consecutive iterations to acquire a stacking configuration from the ultimate displacement subject, minimizing the sum of the intralayer pressure and interlayer adhesion energies within the tip space. This process yields a collection of reconstructed landscapes, characterised by their respective preliminary displacement fields.
The outcomes of our numerical simulations are proven for R- and H-type HBLs with a twist of θ = 0.4° (Fig. 2a,d). The highest two maps illustrate the best moiré and periodically reconstructed patterns, whereas the 4 maps beneath present reconstruction patterns after optimization of preliminary displacement fields that untwist the HBL round a rotation centre indicated by black factors and labelled by a dimensionless coordinate α = 1, 0.5, 0.25, 0. In all instances, optimization yields mesoscopic reconstruction into 2D domains of energetically favoured stackings on the triangle tip (({R}_{h}^{X}) or ({R}_{h}^{M}) and ({H}_{h}^{h}) in R- and H-stacks). These prolonged domains are flanked by 1D stripes, which merge into 0D area arrays.
a,d, Maps of reconstructed domains in triangular suggestions of R-type (a) and H-type (d) heterostacks with a twist angle θ = 0.4° (solely triangle halves are proven within the projections; the size bars are 200 nm). The highest maps present moiré patterns with out reconstruction (delimited by dashed traces from the moiré core of the HBL), whereas the maps beneath present periodic reconstruction and mesoscopically reconstructed area patterns obtained for various zero-twist deformations across the factors marked by black dots at dimensionless positions α (observe that the orange ({R}_{h}^{X}) and inexperienced ({R}_{h}^{M}) domains can interconvert attributable to comparable adhesion energies35). b,e, Whole areal power for R (b) and H (e) at θ = 0.4°, and totally different untwisting factors α (the power of the respective periodic patterns is proven by strong traces). c,f, Whole areal power of periodic and optimally reconstructed (for α = 0) patterns for various twist angles θ in R (c) and H (f) (the power of the respective moiré patterns is indicated by the dashed traces).
As anticipated, optimality reconstructed patterns decrease the full power of the system in response to our simulations proven for R-type (Fig. 2b,c) and H-type (Fig. 2e,f) HBLs. For θ = 0.4°, the full power (normalized by the triangle space) in each stackings is lowered by an element of 10 and a couple of beneath the energies of best moiré and periodic limits, respectively (strong traces in Fig. 2b,e), on reconstruction after optimum rotation at α = 0. The worldwide power minimal—obtained for the rotation level on the borderline between the moiré core and the triangle base—options essentially the most direct transition from the 2D area by 1D stripes to the 0D core. Because the rotation level is moved in direction of the tip (by way of 0 < α < 1), 0D areas emerge on the border and the power acquire decreases, passing the brink of periodic reconstruction at α ≃ 0.5 (0.75) within the R (H) heterostack however remaining effectively beneath the moiré lattice power all through. Remarkably, for the optimally relaxed tip round α = 0, mesoscopic reconstruction stays energetically beneficial for twist angles as much as θ = 3° for each stackings (Fig. 2c,f), in accordance with conclusions from latest Raman spectroscopy research46.
Excitons in reconstructed R-heterostacks
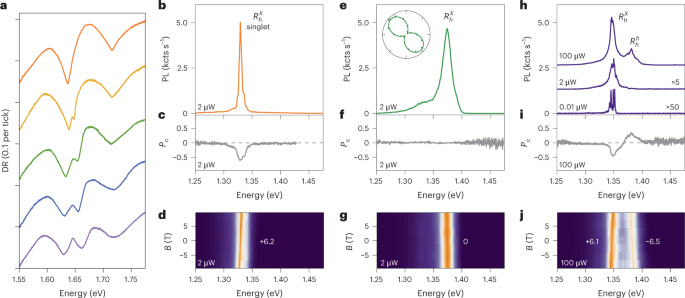
With the instinct for mesoscopic reconstruction, we revisit distinct spectroscopic options of R-stacks within the intralayer and interlayer exciton spectral vary with differential reflection and PL, respectively. The differential reflection spectra—proportional to intralayer exciton absorption—evolve because the remark spot is moved from vibrant to darkish PL areas (Fig. 3a). Following displacement, the differential reflection resonances across the MoSe2 and WSe2 intralayer exciton transitions at 1.64 and 1.71 eV on the intense spots (high spectrum) progressively develop cut up resonances and broadening that’s most pronounced within the darkest areas (backside spectrum). This evolution displays the presence of just one registry in vibrant spots, and modulation of the intralayer exciton power by alternating stackings within the darkest spots. As resonant hybridization in MoSe2–WSe2 heterostacks is strongly inhibited by giant band offsets, multi-peak differential reflection spectra end result from totally different intralayer exciton energies throughout the totally different registries probed by the optical spot.
a, Evolution of differential reflection (DR) spectra of intralayer excitons following gradual displacement from a vibrant to darkish area (proven from high to backside for positions indicated by the black dots in Supplementary Fig. 9a). The height multiplicity is a trademark of nanoscale reconstructed domains. b–d, Interlayer exciton PL (b), Pc (c) and dispersion in a perpendicular magnetic subject B (d), attribute of prolonged 2D domains. The magneto-luminescence information had been recorded underneath linearly polarized excitation with σ+ detection to find out the g-factor values from linear slopes. e–g, Similar as b–d however for areas of 1D stripes with a big diploma of linear polarization (as proven within the inset). h–j, Similar as b–d however in a darkish pattern area of 0D domains (PL spectra proven with offsets and totally different scaling for excitation powers of 100, 2 and 0.01 μW). All information had been recorded on pattern 2 (Supplementary Fig. 9) ; g-factor values with least-square error bars had been obtained from linear matches to the information proven in Supplementary Fig. 16.
Taking into consideration the absence of peak multiplicity within the differential reflection spectra of vibrant spots, the corresponding traits of interlayer exciton PL (Fig. 3b–d) are readily defined. Resulting from regionally prolonged reconstruction, solely lowest-energy ({R}_{h}^{X}) singlet excitons contribute to PL (Fig. 3b), with a peak at 1.33 eV and full-width at half-maximum linewidth of 6 meV, a unfavorable Pc (Fig. 3c) and a constructive g-factor of ~6 (Fig. 3d), as in aligned HBLs21. Such traits are continuously noticed at pattern edges and suggestions (as in Fig. 1c) the place large-scale reconstruction is energetically most beneficial (as within the reconstructed maps of Fig. 2a).
The PL from spatially neighbouring areas is indicative of quantum wire domains44, with blue-shifted emission at round 1.36 eV, a excessive Pl (inset in Fig. 3e), and a vanishing Pc and g-factor worth (Fig. 3f,g). In R-stacks, quantum wires are shaped by alternating optically vibrant ({R}_{h}^{X}) and darkish ({R}_{h}^{M}) domains. The associated 1D confinement of interlayer excitons in stripes of lower-energy ({R}_{h}^{X}) domains flanked by potential partitions of higher-energy ({R}_{h}^{M}) states not solely breaks the threefold rotational symmetry of the exciton wave perform (thereby admixing Okay and ({Okay}^{{prime} }) valleys, and obliterating each Pc and g-factors in perpendicular magnetic subject), it’s also answerable for the blue-shift in PL power. Spot-to-spot variations between pattern areas of excessive Pl, with various orientations of linear polarization axes, are per the variety of stripe geometries. A outstanding instance is the left nook of the R-type triangle in Fig. 1c, during which the intense spot of a big ({R}_{h}^{X}) area with Pc ≃ −1 is encompassed by quantum wire areas with Pl ≃ ±1.
Quantum confinement can be outstanding in R-type areas of 0D arrays which have a lot lowered PL depth and spectrally slender traces at low excitation powers (observe the scaling by 5 and 50 for the spectra at 2 and 0.01 μW, respectively, in Fig. 3h), with attribute unfavorable Pc (Fig. 3i) and g-factors of round ±6 (Supplementary Determine 14b)11. Relying on the precise spot, such quantum dot traces with a full-width at half-maximum effectively beneath 1 meV could be noticed inside spectrally slender or broad home windows of 10 or 100 meV (as seen in Fig. 3h and Fig. 1e, respectively) above the height of prolonged ({R}_{h}^{X}) domains at 1.33 eV. Clearly, areas of 0D arrays enhance the power of interlayer excitons by quantum confinement in nanoscale domains of ({R}_{h}^{X}) stacking, with potential limitations shaped by adjoining ({R}_{h}^{M}) domains, whereas the variations in PL energies relate to totally different strengths of confinement in quantum containers of various dimension.
The spectrally dispersed PL from inhomogenously reconstructed arrays merges at elevated excitation powers (spectra at 2 μW in Figs. 3h and 1e) into structured PL peaks of sub-ensembles grouped by comparable size scales. Reconstructed 0D arrays with lateral homogeneity give rise to a slender ensemble of emission energies (inside 10 meV as in Fig. 3h), which permits us to look at sizzling luminescence with a constructive Pc and unfavorable g-factor of −6.5 (Fig. 3i,j at 100 μW excitation energy). These options—absent within the spectra of 1D and 2D domains—correspond to ({R}_{h}^{h}) singlet interlayer excitons ~50 meV above ({R}_{h}^{X}) states. Such a outstanding contribution of ({R}_{h}^{h}) stacking to the PL is stunning, as principle predicts vanishingly small areas for this non-optimal stacking34,35,36. The sizable PL with ({R}_{h}^{h}) traits due to this fact both implies areas of ({R}_{h}^{h}) domains which can be bigger than anticipated from principle, or that their exciton inhabitants is favoured by population-feeding pathways from excited states or close by ({R}_{h}^{X}) domains.
Excitons in reconstructed H-type heterostacks
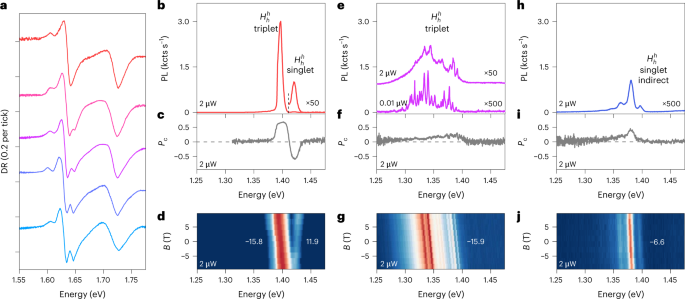
Regardless of similarities, some points of mesoscopic reconstruction in H-type HBLs are distinct. The differential reflection spectra of intralayer excitons within the vibrant and darkish PL areas proven in Fig. 4a (the function at 1.61 eV is because of residual doping on this pattern) result in the identical conclusion as for the R-type spectra of Fig. 3a, that’s, multi-peak intralayer differential reflection resonances in areas of darkish PL are absent within the areas of vibrant PL. For the latter, the atomic registry of reconstructed 2D domains is ({H}_{h}^{h})—unrivalled by different registries by way of energy-optimizing stacking31,34,35. The respective PL spectrum of interlayer excitons (Fig. 4b) is due to this fact easy, that includes solely the emission peaks of triplet and singlet configurations at 1.40 and 1.42 eV with constructive and unfavorable Pc (Fig. 4c), and g-factors of −15.8 and 11.9 (Fig. 4d), respectively21,47,48.
a, Evolution of differential reflection spectra of intralayer excitons following displacement from a vibrant to darkish area (proven from high to backside curves for positions indicated by crimson dots in Supplementary Fig. 10a) with peak multiplicity stemming from reconstructed nanoscale domains. b–j, Interlayer exciton PL (b, e, h), Pc (c, f, i) and B-field dispersion (d, g, j) for 3 consultant positions. The magneto-luminescence information had been recorded underneath linearly polarized excitation with σ+ detection to find out the g-factor values from linear slopes. Spots with vibrant PL (as in b) function triplet and singlet peaks with reverse Pc indicators and attribute g-factors of about −16 and 12. Pattern positions with low PL depth exhibit structured spectra (as in e and h) with lowered Pc. Their traits differ each in spectral profiles and g-factors. Information in e–g are from pattern 2, whereas all different information are from pattern 3 (see Supplementary Fig. 10). The g-factor values with least-square error bars had been obtained from linear matches to the information in Supplementary Fig. 17.
As for R-type HBLs, the differential reflection spectra exhibit an more and more pronounced splitting of the MoSe2 intralayer exciton resonance in darkish areas of H-type samples (backside spectra in Fig. 4a). Within the respective PL spectra (Fig. 4e), for low and average excitation powers (0.01 and a couple of μW, respectively) we once more observe spectrally sharp peaks creating right into a multi-peak ensemble of 0D arrays with an inhomogeneous dimension distribution of nanoscale domains in optimum ({H}_{h}^{h}) stacking. The constructive Pc (Fig. 4f) and the g-factor values (Fig. 4g) verify ({H}_{h}^{h}) stacking because the origin of the emission.
For this stacking, theoretical estimates (Desk 1) place its optically vibrant interlayer exciton states on the high of the power hierarchy above the darkish ({H}_{h}^{M})and ({H}_{h}^{X})states. This energetic ordering is answerable for the absence of 1D options present in R-stacks: excitons in reconstructed ({H}_{h}^{h}) domains usually are not certain by potential limitations that will combine Okay and ({Okay}^{{prime} }) states as in 1D quantum wires of R-stacks (observe the absence of areas with excessive Pl all through the map of H-type triangle in Fig. 1c). Our principle predicts that reconstructed ({H}_{h}^{h}) domains protect luminescent exciton inhabitants on spatially prolonged plateaus, whereas the PL depth decreases in areas of 0D arrays (observe the scaling components of fifty and 500 in Fig. 4e) attributable to inhabitants drain into lower-energy states of the encircling ({H}_{h}^{M})and ({H}_{h}^{X})domains with a lot lowered optical exercise and area areas. Persistently, nanoscale area formation is accompanied by PL red-shifts of as much as 100 meV beneath the ({H}_{h}^{h}) triplet peak at 1.4 eV.
For completeness, in Fig. 4h–j we present the PL traits of a darkish space in an H-stack with about 3° twist. The heterostack shouldn’t be completely vulnerable to reconstruction, with suggestions and edges exhibiting signatures of vibrant ({H}_{h}^{h}) domains (see Supplementary Fig. 10); nonetheless, the darkish areas of the pattern exhibit very totally different options than reconstructed 0D arrays mentioned above, implying that the HBL largely maintains its canonical moiré construction. As proven in Fig. 4h, the PL at 2 μW excitation energy is lowered by one other issue of 10 (observe the scaling issue of 500), with a constructive Pc (Fig. 4i) and a unfavorable g-factor of −6.6 (Fig. 4j) that has no counterpart within the realm of zero-momentum ({Okay}^{{prime} }Okay) interlayer excitons of H-type registries but is attribute of finite-momentum OkayOkay exciton states (see Supplementary Desk 2). The peaks with equidistant power spacing of 16 meV as much as the sixth order (Supplementary Fig. 18) are indicative of interlayer exciton–polaron formation49. On this regime, the heterostructure with layer- and valley-separated excitons dressed by sturdy exciton–phonon coupling is rendered momentum-dark, with luminescent inhabitants decay of exciton–polaron states mediated by a collection of phonon replicas.