Introduction
Comprehending and unleashing the intricate affinities amongst variables within the expansive realm of statistics is integral.
All the things from data-driven decision-making to scientific discoveries to predictive modeling is dependent upon our potential to disentangle the hidden connections and patterns inside advanced datasets. Amongst varied statistical requirements supporting this pursuit, covariance and correlation are essential, rendering insights into the independencies between variables.
Covariance and correlation are ceaselessly occurring variables in statistical evaluation, but folks typically misunderstand or use them interchangeably. The refined nuances differentiating these two requirements can profoundly influence our interpretation and utilization of statistical relationships.
Subsequently, understanding the true nature of Covariance and correlation is paramount for any information fanatic or skilled striving to unveil the total potential of their information.
This blog- covariance vs correlation- will talk about the variations between these two statistical ideas and demystify their relationship.
Additionally, gasoline your information science profession by upgrading your expertise with Analytics Vidhya’s Study Swift for Information Science course.
Covariance
It’s a statistical time period demonstrating a scientific affiliation between two random variables, the place the change within the different mirrors the change in a single variable.
Definition and Calculation of Covariance
Covariance implies whether or not the 2 variables are straight or inversely proportional.
The covariance method determines information factors in a dataset from their common worth. As an example, you may compute the Covariance between two random variables, X and Y, utilizing the next method:

Within the above process,

Decoding Covariance Values
Covariance values point out the magnitude and course (constructive or adverse) of the connection between variables. The covariance values vary from -∞ to +∞. The constructive worth implies a constructive relationship, whereas the adverse worth represents a adverse relationship.
Optimistic, Unfavorable, and Zero Covariance
The upper the quantity, the extra reliant the connection between the variables. Let’s comprehend every variance kind individually:
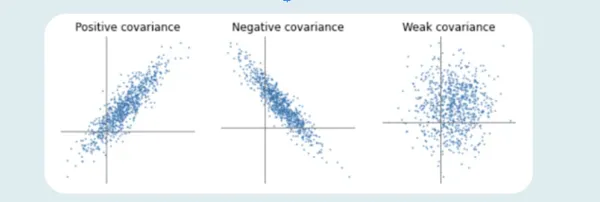
Optimistic Covariance
If the connection between the 2 variables is a constructive covariance, they’re progressing in the identical course. It represents a direct relationship between the variables. Therefore, the variables will behave equally.
The connection between the variables shall be constructive Covariance provided that the values of 1 variable (smaller or extra vital) are equal to the significance of one other variable.
Unfavorable Covariance
A adverse quantity represents adverse Covariance between two random variables. It implies that the variables will share an inverse relationship. In adverse Covariance, the variables transfer in the other way.
In distinction to the constructive Covariance, the higher of 1 variable correspond to the smaller worth of one other variable and vice versa.
Zero Covariance
Zero Covariance signifies no relationship between two variables.
Significance of Covariance in Assessing Linear Relationship
Covariance is important in figuring out the linear relationship between variables. It suggests the course (adverse or constructive) and magnitude of the connection between variables.
The next covariance worth signifies a powerful linear relationship between the variables, whereas a zero covariance suggests no ties.
Limitations and Issues of Covariance
The scales of measurements affect the Covariance and are extremely affected by outliers. Covariance is restricted to measuring solely the linear relationships and doesn’t apprehend the course or energy.
Furthermore, evaluating covariances throughout varied datasets demand warning as a consequence of completely different variable ranges.
Correlation
In contrast to Covariance, correlation tells us the course and energy of the connection between a number of variables. Correlation assesses the extent to which two or extra random variables progress in sequence.
Definition and Calculation of Correlation Coefficient
Correlation is a statistical idea figuring out the connection efficiency of two numerical variables. Whereas deducing the relation between variables, we conclude the change in a single variable that impacts a distinction in one other.
When an identical motion of one other variable reciprocates the development of 1 variable in some method or one other all through the examine of two variables, the variables are correlated.
The method for calculating the correlation coefficient is as follows:
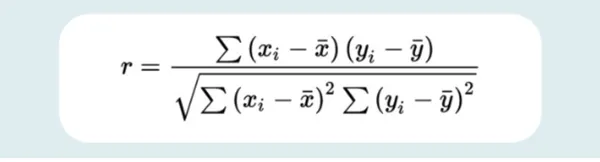
The place,

Decoding Correlation Values
There are three sorts of correlation based mostly on numerous values. Unfavorable correlation, constructive correlation, and no or zero correlation.
Optimistic, Unfavorable, and Zero Correlation
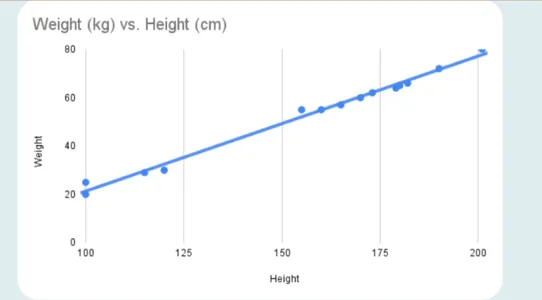
If the variables are straight proportional to 1 one other, the 2 variables are mentioned to carry a constructive correlation. This means that if one variable’s worth rises, the opposite’s worth will exceed. A great constructive correlation possesses a price of 1.
Right here’s what a constructive correlation appears like:
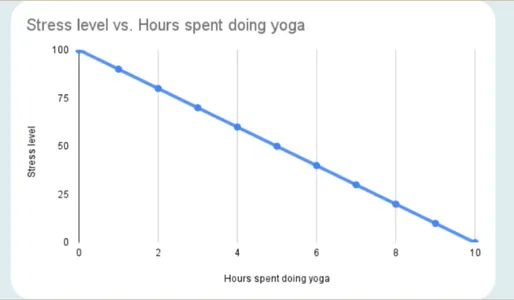
In a adverse correlation, one variable’s worth will increase whereas the second’s worth decreases. An ideal adverse correlation has a price of -1.
The adverse correlation seems as follows:
Identical to within the case of Covariance, a zero correlation means no relation between the variables. Subsequently, whether or not one variable will increase or decreases received’t have an effect on the opposite variable.
Power and Route of Correlation
Correlation assesses the course and energy of a linear relationship between a number of variables. The correlation coefficient varies from -1 to 1, with values close to -1 or 1 implying a excessive affiliation (adverse or constructive, respectively) and values close to 0 suggesting a weak or no correlation.
Pearson Correlation Coefficient and Its Properties
The Pearson correlation coefficient (r) measures the linear connection between two variables. The properties of the Pearson correlation coefficient embrace the next:
- Power: The coefficient’s absolute worth signifies the connection’s energy. The nearer the worth of the coefficient is to 1, the stronger the correlation between variables. Nonetheless, a price nearer to 0 represents a weaker affiliation.
- Route: The coefficient’s signal denotes the course of the connection. If the worth is constructive, there’s a constructive correlation between the 2 variables, which signifies that if one variable rises, the opposite may even rise. If the worth is adverse, there’s a adverse correlation, which means that when one variable will increase, the opposite will fall.
- Vary: The coefficient’s content material varies from -1 to 1. The proper linear relationship is represented by a number of -1, the absence of a linear relationship is represented by 0, and a great linear relationship is denoted by a price of 1.
- Independence: The Pearson correlation coefficient quantifies how linearly dependent two variables are however doesn’t indicate causality. There isn’t a assure {that a} robust correlation signifies a cause-and-effect connection.
- Linearity: The Pearson correlation coefficient solely assesses linear relationships between variables. The coefficient might be inadequate to explain non-linear connections totally.
- Sensitivity to Outliers: Outliers within the information may affect the correlation coefficient’s worth, thereby boosting or deflating its measurement.
In order for you hands-on expertise engaged on Information Science tasks, discover a complete program by Analytics Vidhya on Prime Information Science Initiatives for Analysts and Information Scientists.
Different Sorts of Correlation Coefficients
Different correlation coefficients are:
- Spearman’s Rank Correlation: It’s a nonparametric indicator of rank correlation or the statistical dependency between the ranks of two variables. It evaluates how successfully a monotonic operate can seize the connection between two variables.
- Kendall Rank Correlation: A statistic determines the ordinal relationship between two measured values. It represents the similarity of the info orderings when ordered by every amount, which is a measure of rank correlation.
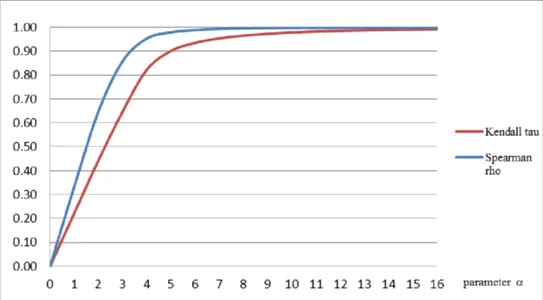
A picture of an anti-symmetric household of copulas’ Spearman rank correlation and Kendall’s tau are inherently odd parameter features.
Benefits and Disadvantages of Covariance
Following are the benefits and drawbacks of Covariance:
Benefits
- Straightforward to Calculate: Calculating covariance doesn’t require any assumptions of the underlying information distribution. Therefore, it’s straightforward to calculate covariance with the method given above.
- Apprehends Relationship: Covariance gauges the extent of linear affiliation between variables, furnishing details about the connection’s magnitude and course (constructive or adverse).
- Useful in Portfolio Evaluation: Covariance is usually employed in portfolio evaluation to judge the diversification benefits of integrating completely different property.
Disadvantages
- Restricted to Linear Relationships: Covariance solely gauges linear relationships between variables and doesn’t seize non-linear associations.
- Doesn’t Provide Relationship Magnitude: Covariance doesn’t provide a standardized estimation of the depth or energy of the connection between variables.
- Scale Dependency: Covariance is affected by the variables’ measurement scales, making evaluating covariances throughout varied datasets or variables with distinct models difficult.
Benefits and Disadvantages of Correlation
The benefits and drawbacks of correlation are as follows:
Benefits
- Figuring out Non-Linear Relationships: Whereas correlation primarily estimates linear relationships, it might additionally display the presence of non-linear connections, particularly when utilizing various correlation requirements like Spearman’s rank correlation coefficient.
- Standardized Criterion: Correlation coefficients, such because the Pearson correlation coefficient, are standardized, various from -1 to 1. This permits for straightforward comparability and interpretation of the course and energy of relationships throughout completely different datasets.
- Robustness to Outliers: Correlation coefficients are sometimes much less delicate to outliers than Covariance, delivering a stronger normal of the affiliation between variables.
- Scale Independencies: Correlation just isn’t affected by the measurement scales, making it handy for evaluating affinities between variables with distinct models or scales.
Disadvantages
- Pushed by Excessive Values: Excessive values can nonetheless have an effect on the correlation coefficient, despite the fact that it’s much less inclined to outliers than Covariance.
- Information Necessities: Correlation assumes that the info is distributed in accordance with a bivariate regular distribution, which can not at all times be correct.
- Restricted to Bivariate Evaluation: As a result of correlation solely examines the connection between two variables concurrently, it might solely seize easy multivariate correlations.
Similarities between Covariance and Correlation
Covariance vs correlation positive has a number of variations, however they’ve similarities too. A few of the similarities are as follows:
Indicators of the Relationship between Variables
Correlation and Covariance each gauge simply the linear relationship between variables. This means that if the correlation coefficient is zero, so will the Covariance. Even the change in location doesn’t have an effect on the correlation and covariance requirements.
The Measure of Linear Affiliation
Each Covariance and correlation are measures used to evaluate the connection between variables. They provide readability on how variables are linked to 1 one other.
Calculations Utilizing the Identical Variables
The calculation of Covariance and correlation each require the identical set of variables. They want
Covariance and correlation calculations contain the identical set of variables. They require paired observations of the variables of curiosity to find out their relationship.
Nonetheless, if it’s about selecting between Covariance and correlation to reckon the connection between variables, specialists at all times choose correlation over Covariance as a result of the change in scale doesn’t have an effect on correlation.
Variations between Covariance and Correlation
Whereas each of them are statistical phrases, Covariance and correlation differ from one another on varied grounds.
Interpretation and Scale of Values
The change in scale adjustments the worth of Covariance. The next quantity in Covariance means greater dependency. Decoding Covariance is troublesome.
Quite the opposite, the correlation worth stays unaffected by the change in scale. The correlation coefficients vary from -1 to 1, which permits for a extra simple interpretation, not like Covariance.
Relationship to the Models of Measurement
The variables’ measurement models have an effect on Covariance, making evaluating covariance values throughout varied datasets or variables with completely different models difficult.
However, correlation coefficients don’t have any models and don’t depend on the models of measurement, permitting comparisons between variables with varied models.
Standardization and Comparability Throughout Datasets
Since Covariance doesn’t have standardization, evaluating covariances throughout varied datasets is difficult. Whereas correlation coefficients are standardized. Subsequently, evaluating it straight throughout variables, datasets, or contexts is simple.
Robustness to Outliers
Outlier massively impacts the worth of Covariance. Therefore, it’s delicate to the presence of outliers. Quite the opposite, correlation coefficients provide a extra sturdy normal of the connection between variables, as correlation coefficients are much less inclined to outliers.
Utilization in Totally different Contexts and Purposes
Covariance has purposes within the following:
- Biology — Molecular and Genetics to gauge particular DNAs.
- Estimating the invested quantity on completely different property in monetary markets.
- Gathering information procured from oceanographic/astronomical research to conclude.
- Analyzing a dataset with logical implications of the principal component.
- Finding out alerts obtained in numerous kinds.
However, the correlation has the next purposes:
- Employed in sample recognition
- Measures the connection between poverty and inhabitants
- Analyzes temperature rise throughout summer season v/s water consumption amongst relations
- Estimates the time vs. cash a buyer has spent on a web-based e-commerce web site
- Compares the previous climate forecast stories to the present yr.
To summarize the variations, right here’s a desk you need to look by:
| Distinction Grounds | Covariance | Correlation |
| That means | Covariance means two variables straight or inversely rely on each other. | Two variables are mentioned to be in correlation if the change in a single impacts the opposite variable. |
| Values | Lie between -infinity to +infinity | Values lie between -1 to 1 |
| Unit | It’s a product of the unit of variables | It’s a unit-free measure |
| Change in Scale | Even minor adjustments in scale have an effect on Covariance | There received’t be any change in correlation due to the dimensions |
| Measure of | Correlation | The scaled model of Covariance |
| Utility | Market Analysis, Portfolio Evaluation, and Danger Help | Medical Analysis, Information Evaluation, and Forecasting |
Use Instances and Examples
Given beneath are some sensible purposes and examples of Covariance vs Correlation:
Sensible Situations The place Covariance is Helpful
There are three sensible eventualities the place Covariance proves useful:
- Market Analysis: Covariance is employed in market analysis for analyzing the hyperlink between variables, reminiscent of gross sales income and promoting expenditure, to understand the affect of selling endeavors on enterprise outcomes.
- Danger Evaluation: Covariance helps in threat administration and threat evaluation. As an example, in insurance coverage, Covariance will help establish the affiliation between distinct variables (reminiscent of claims frequency, well being circumstances, and age) to evaluate potential losses and set acceptable premiums.
- Portfolio Evaluation: Covariance has a profound utility in finance for evaluating the connection between completely different asset returns inside a portfolio. A constructive covariance signifies that the property will transfer in the identical course, whereas a adverse one signifies that they are going to go in reverse instructions. Such info is useful in portfolio diversification for managing threat.
Sensible Situations The place Correlation is Helpful
Some sensible circumstances of correlation embrace forecasting, information evaluation, and medical analysis.
- Forecasting: Correlations support forecasters in figuring out the diploma to which they will predict one variable based mostly on the values of one other variable. For instance, correlation in gross sales forecasting may be useful in foretelling future gross sales based mostly on earlier gross sales data.
- Evaluation of Information: Information fanatics use correlation popularly to quantify and establish relationships between variables. As an example, in social sciences, correlation will help decide the hyperlink between variables like training degree or revenue or between productiveness and job satisfaction.
- Medical Analysis: In medical analysis, correlations assist discover associations between variables, just like the correlation between lung most cancers and smoking or the correlation between the chance of cardiovascular illnesses and the BMI (physique mass index).
Actual-World Examples and Purposes of Covariance and Correlation
Whereas the purposes of Covariance and correlation have been described above, some real-world examples of the identical are as follows:
Covariances are used extensively in finance and present-day portfolio concept. As an example, the Covariance between safety and the market are utilized within the calculation for one of many mannequin’s key variables, beta, within the capital asset pricing mannequin (CAPM), which determines the anticipated return on an asset.
Within the CAPM, beta quantifies an asset’s volatility, or systematic threat, in comparison with the entire market; it’s a beneficial metric that makes use of Covariance to find out an investor’s threat publicity explicit to 1 funding.
Examples of Correlation embrace the time spent operating vs. the physique fats. The extra time an individual spends jogging, the much less physique fats they’ve. In different phrases, a adverse relationship exists between variable operating time and variable physique fats. Physique fats lowers as operating time rises.
One other occasion contains physique weight vs. top. The connection between a person’s measurement and weight is often upbeat. In different phrases, those that are taller are likely to weigh extra.
Factors to Think about Whereas Selecting Between Covariance and Correlation
Earlier than concluding or selecting Covariance or correlation, you need to preserve the next into consideration:
1. Issues for the Analysis Query or Goal
Focus in your necessities. No matter you select should go along with the particular goal or analysis query. In case you purpose to estimate the course and energy of the linear affiliation between variables, then choosing the correlation shall be smart. Nonetheless, in the event you want to measure the extent of a relationship with none interpretation, go for Covariance.
2. Nature of the Variables and Underlying Assumptions
The following level to contemplate is the character of the variables you’re inspecting and the assumptions for every measure. The Correlation has no unit; it’s unitless and embraces a linear affiliation between variables. Nonetheless, Covariance focuses on the fundamental models and is delicate to the dimensions.
3. Availability of Information and Measurement Scale
Don’t forget to evaluate the variable’s measurement scale and the accessible information. Whereas Covariance calls for paired observations of the variables, the correlation wants the same and bivariate normality assumption.
4. Significance of Standardized Interpretation or Comparability
You will need to analyze the necessity for comparability or standardized interpretation throughout varied variables or units of information. If the comparability is crucial, the standardized vary of correlation varies from -1 to 1, permitting for easy comparability and interpretation.
5. Applicability within the Particular Evaluation or Area
You will need to select a specific evaluation or subject of analysis. Whereas Covariance is relevant in market analysis, threat evaluation, and finance, correlation is employed in forecasting, information evaluation, and social sciences.
Conclusion
Understanding the variations between Covariance and correlation is important. Covariance measures the diploma of linear relationship, whereas correlation provides a standardized measurement that additionally considers the course and energy of the connection.
Covariance vs correlation has a number of grounds for differentiation, reminiscent of standardization, interpretation, scale, sensitivity to outliers, and purposes in varied phrases. Whereas they differ considerably, they do share some similarities as properly. They’re indicators of the connection between variables and measures of linear affiliation.
Selecting an acceptable measure is essential. It needs to be based mostly on particular necessities and the context of the evaluation. Covariance is useful in market analysis, threat evaluation, portfolio evaluation, and extra. In distinction, correlation is useful in medical analysis, forecasting, information evaluation, and different areas.
Why not do it with specialists if you wish to speed up your profession? Discover Analytics Vidhya’s Information Science Hacks, Ideas, and Methods course to sharpen your information science expertise and seize a rewarding profession as an information scientist.
Steadily Requested Questions
A. A constructive covariance implies that two variables are transferring in the identical course. It signifies a direct hyperlink between the variables. It means if the worth of 1 variable is extra wonderful, the worth of one other variable may even be related.
A. The adverse Covariance means that the variables will share an inverse relationship. In adverse Covariance, the variables progress in the other way. This additionally signifies that if one worth has an above-average worth, the opposite could have a below-average worth.
A. The correlation coefficient of 1 means a great constructive linear relationship between the variables. It means that if one variable will increase, one other one may even enhance.
A. A correlation coefficient of 0 suggests no linear affiliation between the variables. It signifies that even when one variable adjustments, one other will stay unaffected.
A. Covariance and correlation matrices provide insights into the relationships between varied variables in an information set.

