Final Up to date on November 15, 2022
Derivatives are one of the vital basic ideas in calculus. They describe how modifications within the variable inputs have an effect on the operate outputs. The target of this text is to offer a high-level introduction to calculating derivatives in PyTorch for many who are new to the framework. PyTorch gives a handy option to calculate derivatives for user-defined capabilities.
Whereas we all the time need to take care of backpropagation (an algorithm recognized to be the spine of a neural community) in neural networks, which optimizes the parameters to reduce the error as a way to obtain greater classification accuracy; ideas discovered on this article can be utilized in later posts on deep studying for picture processing and different pc imaginative and prescient issues.
After going via this tutorial, you’ll be taught:
- How one can calculate derivatives in PyTorch.
- How one can use autograd in PyTorch to carry out auto differentiation on tensors.
- In regards to the computation graph that includes completely different nodes and leaves, permitting you to calculate the gradients in a easy attainable method (utilizing the chain rule).
- How one can calculate partial derivatives in PyTorch.
- How one can implement the spinoff of capabilities with respect to a number of values.
Let’s get began.

Calculating Derivatives in PyTorch
Image by Jossuha Théophile. Some rights reserved.
Differentiation in Autograd
The autograd – an auto differentiation module in PyTorch – is used to calculate the derivatives and optimize the parameters in neural networks. It’s supposed primarily for gradient computations.
Earlier than we begin, let’s load up some obligatory libraries we’ll use on this tutorial.
|
import matplotlib.pyplot as plt import torch |
Now, let’s use a easy tensor and set the requires_grad parameter to true. This enables us to carry out computerized differentiation and lets PyTorch consider the derivatives utilizing the given worth which, on this case, is 3.0.
|
x = torch.tensor(3.0, requires_grad = True) print(“making a tensor x: “, x) |
|
making a tensor x: tensor(3., requires_grad=True) |
We’ll use a easy equation $y=3x^2$ for instance and take the spinoff with respect to variable x. So, let’s create one other tensor in line with the given equation. Additionally, we’ll apply a neat methodology .backward on the variable y that varieties acyclic graph storing the computation historical past, and consider the outcome with .grad for the given worth.
|
y = 3 * x ** 2 print(“Results of the equation is: “, y) y.backward() print(“Dervative of the equation at x = 3 is: “, x.grad) |
|
Results of the equation is: tensor(27., grad_fn=<MulBackward0>) Dervative of the equation at x = 3 is: tensor(18.) |
As you may see, we have now obtained a worth of 18, which is appropriate.
Computational Graph
PyTorch generates derivatives by constructing a backwards graph behind the scenes, whereas tensors and backwards capabilities are the graph’s nodes. In a graph, PyTorch computes the spinoff of a tensor relying on whether or not it’s a leaf or not.
PyTorch won’t consider a tensor’s spinoff if its leaf attribute is about to True. We gained’t go into a lot element about how the backwards graph is created and utilized, as a result of the purpose right here is to offer you a high-level information of how PyTorch makes use of the graph to calculate derivatives.
So, let’s test how the tensors x and y look internally as soon as they’re created. For x:
|
print(‘information attribute of the tensor:’,x.information) print(‘grad attribute of the tensor::’,x.grad) print(‘grad_fn attribute of the tensor::’,x.grad_fn) print(“is_leaf attribute of the tensor::”,x.is_leaf) print(“requires_grad attribute of the tensor::”,x.requires_grad) |
|
information attribute of the tensor: tensor(3.) grad attribute of the tensor:: tensor(18.) grad_fn attribute of the tensor:: None is_leaf attribute of the tensor:: True requires_grad attribute of the tensor:: True |
and for y:
|
print(‘information attribute of the tensor:’,y.information) print(‘grad attribute of the tensor:’,y.grad) print(‘grad_fn attribute of the tensor:’,y.grad_fn) print(“is_leaf attribute of the tensor:”,y.is_leaf) print(“requires_grad attribute of the tensor:”,y.requires_grad) |
|
print(‘information attribute of the tensor:’,y.information) print(‘grad attribute of the tensor:’,y.grad) print(‘grad_fn attribute of the tensor:’,y.grad_fn) print(“is_leaf attribute of the tensor:”,y.is_leaf) print(“requires_grad attribute of the tensor:”,y.requires_grad) |
As you may see, every tensor has been assigned with a specific set of attributes.
The information attribute shops the tensor’s information whereas the grad_fn attribute tells in regards to the node within the graph. Likewise, the .grad attribute holds the results of the spinoff. Now that you’ve got learnt some fundamentals in regards to the autograd and computational graph in PyTorch, let’s take slightly extra difficult equation $y=6x^2+2x+4$ and calculate the spinoff. The spinoff of the equation is given by:
$$frac{dy}{dx} = 12x+2$$
Evaluating the spinoff at $x = 3$,
$$left.frac{dy}{dx}rightvert_{x=3} = 12times 3+2 = 38$$
Now, let’s see how PyTorch does that,
|
x = torch.tensor(3.0, requires_grad = True) y = 6 * x ** 2 + 2 * x + 4 print(“Results of the equation is: “, y) y.backward() print(“By-product of the equation at x = 3 is: “, x.grad) |
|
Results of the equation is: tensor(64., grad_fn=<AddBackward0>) By-product of the equation at x = 3 is: tensor(38.) |
The spinoff of the equation is 38, which is appropriate.
Implementing Partial Derivatives of Features
PyTorch additionally permits us to calculate partial derivatives of capabilities. For instance, if we have now to use partial derivation to the next operate,
$$f(u,v) = u^3+v^2+4uv$$
Its spinoff with respect to $u$ is,
$$frac{partial f}{partial u} = 3u^2 + 4v$$
Equally, the spinoff with respect to $v$ can be,
$$frac{partial f}{partial v} = 2v + 4u$$
Now, let’s do it the PyTorch manner, the place $u = 3$ and $v = 4$.
We’ll create u, v and f tensors and apply the .backward attribute on f as a way to compute the spinoff. Lastly, we’ll consider the spinoff utilizing the .grad with respect to the values of u and v.
|
u = torch.tensor(3., requires_grad=True) v = torch.tensor(4., requires_grad=True)
f = u**3 + v**2 + 4*u*v
print(u) print(v) print(f)
f.backward() print(“Partial spinoff with respect to u: “, u.grad) print(“Partial spinoff with respect to v: “, v.grad) |
|
tensor(3., requires_grad=True) tensor(4., requires_grad=True) tensor(91., grad_fn=<AddBackward0>) Partial spinoff with respect to u: tensor(43.) Partial spinoff with respect to v: tensor(20.) |
By-product of Features with A number of Values
What if we have now a operate with a number of values and we have to calculate the spinoff with respect to its a number of values? For this, we’ll make use of the sum attribute to (1) produce a scalar-valued operate, after which (2) take the spinoff. That is how we are able to see the ‘operate vs. spinoff’ plot:
|
# compute the spinoff of the operate with a number of values x = torch.linspace(–20, 20, 20, requires_grad = True) Y = x ** 2 y = torch.sum(Y) y.backward()
# ploting the operate and spinoff function_line, = plt.plot(x.detach().numpy(), Y.detach().numpy(), label = ‘Perform’) function_line.set_color(“crimson”) derivative_line, = plt.plot(x.detach().numpy(), x.grad.detach().numpy(), label = ‘By-product’) derivative_line.set_color(“inexperienced”) plt.xlabel(‘x’) plt.legend() plt.present() |
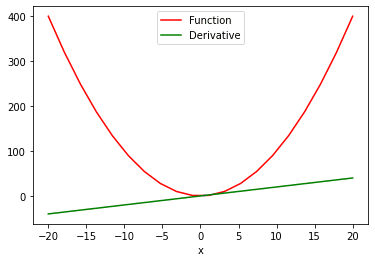
Within the two plot() operate above, we extract the values from PyTorch tensors so we are able to visualize them. The .detach methodology doesn’t permit the graph to additional monitor the operations. This makes it straightforward for us to transform a tensor to a numpy array.
Abstract
On this tutorial, you discovered the right way to implement derivatives on varied capabilities in PyTorch.
Notably, you discovered:
- How one can calculate derivatives in PyTorch.
- How one can use autograd in PyTorch to carry out auto differentiation on tensors.
- In regards to the computation graph that includes completely different nodes and leaves, permitting you to calculate the gradients in a easy attainable method (utilizing the chain rule).
- How one can calculate partial derivatives in PyTorch.
- How one can implement the spinoff of capabilities with respect to a number of values.

