A novel differentially personal aggregation framework – Google AI Weblog

Differential privateness (DP) machine studying algorithms shield person information by limiting the impact of every information level on an aggregated output with a mathematical assure. Intuitively the assure implies that altering a single person’s contribution shouldn’t considerably change the output distribution of the DP algorithm.

Nevertheless, DP algorithms are typically much less correct than their non-private counterparts as a result of satisfying DP is a worst-case requirement: one has so as to add noise to “cover” modifications in any potential enter level, together with “unlikely factors’’ which have a major impression on the aggregation. For instance, suppose we need to privately estimate the typical of a dataset, and we all know {that a} sphere of diameter, Λ, incorporates all potential information factors. The sensitivity of the typical to a single level is bounded by Λ, and subsequently it suffices so as to add noise proportional to Λ to every coordinate of the typical to make sure DP.

A sphere of diameter Λ containing all potential information factors.

Now assume that each one the information factors are “pleasant,” which means they’re shut collectively, and every impacts the typical by at most 𝑟, which is far smaller than Λ. Nonetheless, the standard means for making certain DP requires including noise proportional to Λ to account for a neighboring dataset that incorporates one extra “unfriendly” level that’s unlikely to be sampled.

Two adjoining datasets that differ in a single outlier. A DP algorithm must add noise proportional to Λ to every coordinate to cover this outlier.

In “FriendlyCore: Sensible Differentially Non-public Aggregation”, offered at ICML 2022, we introduce a basic framework for computing differentially personal aggregations. The FriendlyCore framework pre-processes information, extracting a “pleasant” subset (the core) and consequently decreasing the personal aggregation error seen with conventional DP algorithms. The personal aggregation step provides much less noise since we don’t must account for unfriendly factors that negatively impression the aggregation.

Within the averaging instance, we first apply FriendlyCore to take away outliers, and within the aggregation step, we add noise proportional to 𝑟 (not Λ). The problem is to make our general algorithm (outlier removing + aggregation) differentially personal. This constrains our outlier removing scheme and stabilizes the algorithm in order that two adjoining inputs that differ by a single level (outlier or not) ought to produce any (pleasant) output with related chances.

FriendlyCore Framework

We start by formalizing when a dataset is taken into account pleasant, which is determined by the kind of aggregation wanted and may seize datasets for which the sensitivity of the combination is small. For instance, if the combination is averaging, the time period pleasant ought to seize datasets with a small diameter.

To summary away the actual software, we outline friendliness utilizing a predicate 𝑓 that’s optimistic on factors 𝑥 and 𝑦 if they’re “shut” to one another. For instance,within the averaging software 𝑥 and 𝑦 are shut if the space between them is lower than 𝑟. We are saying {that a} dataset is pleasant (for this predicate) if each pair of factors 𝑥 and 𝑦 are each near a 3rd level 𝑧 (not essentially within the information).

As soon as we now have mounted 𝑓 and outlined when a dataset is pleasant, two duties stay. First, we assemble the FriendlyCore algorithm that extracts a big pleasant subset (the core) of the enter stably. FriendlyCore is a filter satisfying two necessities: (1) It has to take away outliers to maintain solely components which might be near many others within the core, and (2) for neighboring datasets that differ by a single aspect, 𝑦, the filter outputs every aspect besides 𝑦 with nearly the identical chance. Moreover, the union of the cores extracted from these neighboring datasets is pleasant.

The concept underlying FriendlyCore is straightforward: The chance that we add a degree, 𝑥, to the core is a monotonic and steady operate of the variety of components near 𝑥. Particularly, if 𝑥 is near all different factors, it’s not thought of an outlier and might be stored within the core with chance 1.

Second, we develop the Pleasant DP algorithm that satisfies a weaker notion of privateness by including much less noise to the combination. Which means that the outcomes of the aggregation are assured to be related just for neighboring datasets 𝐶 and 𝐶’ such that the union of 𝐶 and 𝐶’ is pleasant.

Our most important theorem states that if we apply a pleasant DP aggregation algorithm to the core produced by a filter with the necessities listed above, then this composition is differentially personal within the common sense.

Clustering and different purposes

Different purposes of our aggregation technique are clustering and studying the covariance matrix of a Gaussian distribution. Contemplate using FriendlyCore to develop a differentially personal k-means clustering algorithm. Given a database of factors, we partition it into random equal-size smaller subsets and run a great non-private okay-means clustering algorithm on every small set. If the unique dataset incorporates okay giant clusters then every smaller subset will comprise a major fraction of every of those okay clusters. It follows that the tuples (ordered units) of okay-centers we get from the non-private algorithm for every small subset are related. This dataset of tuples is predicted to have a big pleasant core (for an acceptable definition of closeness).

We use our framework to combination the ensuing tuples of okay-centers (okay-tuples). We outline two such okay-tuples to be shut if there’s a matching between them such {that a} heart is considerably nearer to its mate than to some other heart.

On this image, any pair of the purple, blue, and inexperienced tuples are shut to one another, however none of them is near the pink tuple. So the pink tuple is eliminated by our filter and isn’t within the core.

We then extract the core by our generic sampling scheme and combination it utilizing the next steps:

1. Decide a random okay-tuple 𝑇 from the core.
2. Partition the information by placing every level in a bucket based on its closest heart in 𝑇.
3. Privately common the factors in every bucket to get our closing okay-centers.

Empirical outcomes

Beneath are the empirical outcomes of our algorithms primarily based on FriendlyCore. We applied them within the zero-Concentrated Differential Privateness (zCDP) mannequin, which supplies improved accuracy in our setting (with related privateness ensures because the extra well-known (𝜖, 𝛿)-DP).

Averaging

We examined the imply estimation of 800 samples from a spherical Gaussian with an unknown imply. We in contrast it to the algorithm CoinPress. In distinction to FriendlyCore, CoinPress requires an higher certain 𝑅 on the norm of the imply. The figures beneath present the impact on accuracy when growing 𝑅 or the dimension 𝑑. Our averaging algorithm performs higher on giant values of those parameters since it’s unbiased of 𝑅 and 𝑑.

Clustering

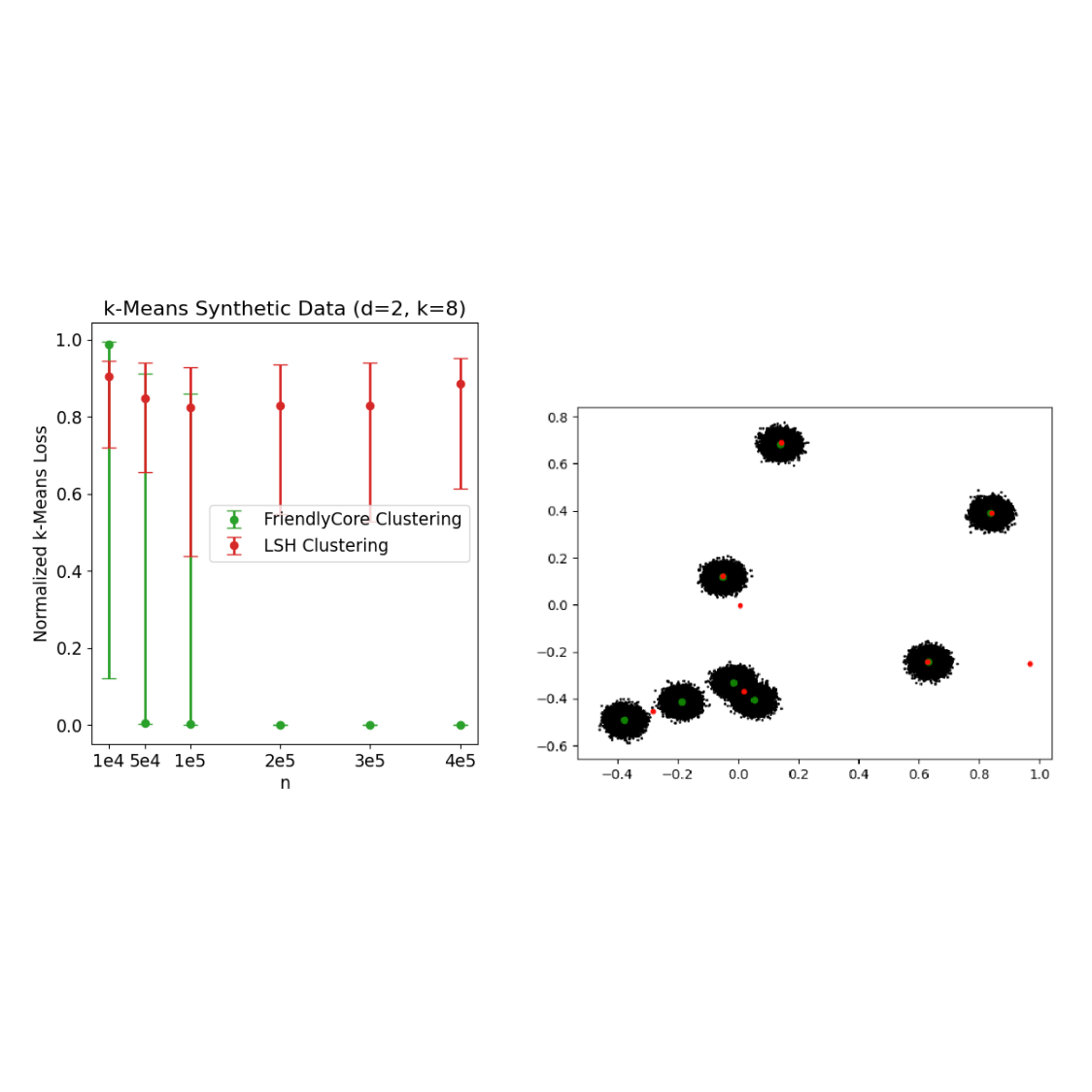
We examined the efficiency of our personal clustering algorithm for okay-means. We in contrast it to the Chung and Kamath algorithm that’s primarily based on recursive locality-sensitive hashing (LSH-clustering). For every experiment, we carried out 30 repetitions and current the medians together with the 0.1 and 0.9 quantiles. In every repetition, we normalize the losses by the lack of k-means++ (the place a smaller quantity is best).

The left determine beneath compares the okay-means outcomes on a uniform combination of eight separated Gaussians in two dimensions. For small values of 𝑛 (the variety of samples from the combination), FriendlyCore typically fails and yields inaccurate outcomes. But, growing 𝑛 will increase the success chance of our algorithm (as a result of the generated tuples turn out to be nearer to one another) and yields very correct outcomes, whereas LSH-clustering lags behind.

Left: okay-means ends in 𝑑= 2 and okay= 8, for various 𝑛(variety of samples). Proper: A graphical illustration of the facilities in one of many iterations for 𝑛= 2 X 105. Inexperienced factors are the facilities of our algorithm and the purple factors are the facilities of LSH-clustering.

FriendlyCore additionally performs effectively on giant datasets, even with out clear separation into clusters. We used the Fonollosa and Huerta fuel sensors dataset that incorporates 8M rows, consisting of a 16-dimensional level outlined by 16 sensors’ measurements at a given time limit. We in contrast the clustering algorithms for various okay. FriendlyCore performs effectively apart from okay= 5 the place it fails as a result of instability of the non-private algorithm utilized by our technique (there are two completely different options for okay= 5 with related price that makes our method fail since we don’t get one set of tuples which might be shut to one another).

okay-means outcomes on fuel sensors’ measurements over time, various okay.

Conclusion

FriendlyCore is a basic framework for filtering metric information earlier than privately aggregating it. The filtered information is steady and makes the aggregation much less delicate, enabling us to extend its accuracy with DP. Our algorithms outperform personal algorithms tailor-made for averaging and clustering, and we consider this method might be helpful for added aggregation duties. Preliminary outcomes present that it might successfully scale back utility loss once we deploy DP aggregations. To study extra, and see how we apply it for estimating the covariance matrix of a Gaussian distribution, see our paper.

Acknowledgements

This work was led by Eliad Tsfadia in collaboration with Edith Cohen, Haim Kaplan, Yishay Mansour, Uri Stemmer, Avinatan Hassidim and Yossi Matias.