Within the first publish on this collection, we launched using hashing strategies to detect related capabilities in reverse engineering eventualities. We described PIC hashing, the hashing approach we use in SEI Pharos, in addition to some terminology and metrics to judge how properly a hashing approach is working. We left off final time after displaying that PIC hashing performs poorly in some instances, and puzzled aloud whether it is potential to do higher.
On this publish, we’ll attempt to reply that query by introducing and experimenting with a really totally different sort of hashing referred to as fuzzy hashing. Like common hashing, there’s a hash operate that reads a sequence of bytes and produces a hash. In contrast to common hashing, although, you do not examine fuzzy hashes with equality. As an alternative, there’s a similarity operate that takes two fuzzy hashes as enter and returns a quantity between 0 and 1, the place 0 means utterly dissimilar and 1 means utterly related.
My colleague, Cory Cohen, and I debated whether or not there may be utility in making use of fuzzy hashes to instruction bytes, and our debate motivated this weblog publish. I assumed there could be a profit, however Cory felt there wouldn’t. Therefore, these experiments. For this weblog publish, I will be utilizing the Lempel-Ziv Jaccard Distance fuzzy hash (LZJD) as a result of it is quick, whereas most fuzzy hash algorithms are sluggish. A quick fuzzy hashing algorithm opens up the potential of utilizing fuzzy hashes to seek for related capabilities in a big database and different fascinating potentialities.
As a baseline I will even be utilizing Levenshtein distance, which is a measure of what number of modifications it is advisable to make to 1 string to rework it to a different. For instance, the Levenshtein distance between “cat” and “bat” is 1, since you solely want to alter the primary letter. Levenshtein distance permits us to outline an optimum notion of similarity on the instruction byte degree. The tradeoff is that it is actually sluggish, so it is solely actually helpful as a baseline in our experiments.
Experiments in Accuracy of PIC Hashing and Fuzzy Hashing
To check the accuracy of PIC hashing and fuzzy hashing beneath numerous eventualities, I outlined just a few experiments. Every experiment takes an analogous (or an identical) piece of supply code and compiles it, typically with totally different compilers or flags.
Experiment 1: openssl model 1.1.1w
On this experiment, I compiled openssl model 1.1.1w in just a few alternative ways. In every case, I examined the ensuing openssl executable.
Experiment 1a: openssl1.1.1w Compiled With Completely different Compilers
On this first experiment, I compiled openssl 1.1.1w with gcc -O3 -g and clang -O3 -g and in contrast the outcomes. We’ll begin with the confusion matrix for PIC hashing:
|
|
|
|
|
|
|
|
|
|
|
|
As we noticed earlier, this leads to a recall of 0.07, a precision of 0.45, and a F1 rating of 0.12. To summarize: fairly dangerous.
How do LZJD and Levenshtein distance do? Properly, that is a bit tougher to quantify, as a result of now we have to choose a similarity threshold at which we contemplate the operate to be “the identical.” For instance, at a threshold of 0.8, we might contemplate a pair of capabilities to be the identical if that they had a similarity rating of 0.8 or increased. To speak this data, we may output a confusion matrix for every potential threshold. As an alternative of doing this, I will plot the outcomes for a spread of thresholds proven in Determine 1 under:
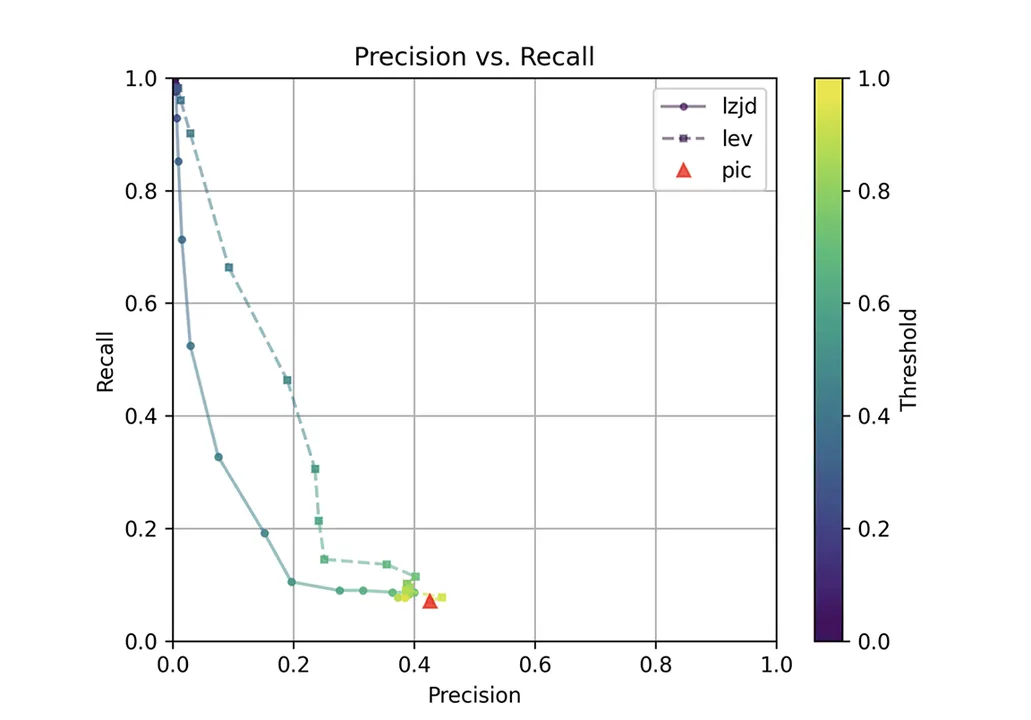
Determine 1: Precision Versus Recall Plot for “openssl GCC vs. Clang
The pink triangle represents the precision and recall of PIC hashing: 0.45 and 0.07 respectively, identical to we calculated above. The stable line represents the efficiency of LZJD, and the dashed line represents the efficiency of Levenshtein distance (LEV). The colour tells us what threshold is getting used for LZJD and LEV. On this graph, the best consequence could be on the prime proper (100% recall and precision). So, for LZJD and LEV to have a bonus, it needs to be above or to the best of PIC hashing. However, we are able to see that each LZJD and LEV go sharply to the left earlier than transferring up, which signifies {that a} substantial lower in precision is required to enhance recall.
Determine 2 illustrates what I name the violin plot. You could need to click on on it to zoom in. There are three panels: The leftmost is for LEV, the center is for PIC hashing, and the rightmost is for LZJD. On every panel, there’s a True column, which exhibits the distribution of similarity scores for equal pairs of capabilities. There may be additionally a False column, which exhibits the distribution scores for nonequivalent pairs of capabilities. Since PIC hashing doesn’t present a similarity rating, we contemplate each pair to be both equal (1.0) or not (0.0). A horizontal dashed line is plotted to indicate the brink that has the best F1 rating (i.e., mixture of each precision and recall). Inexperienced factors point out operate pairs which are appropriately predicted as equal or not, whereas pink factors point out errors.
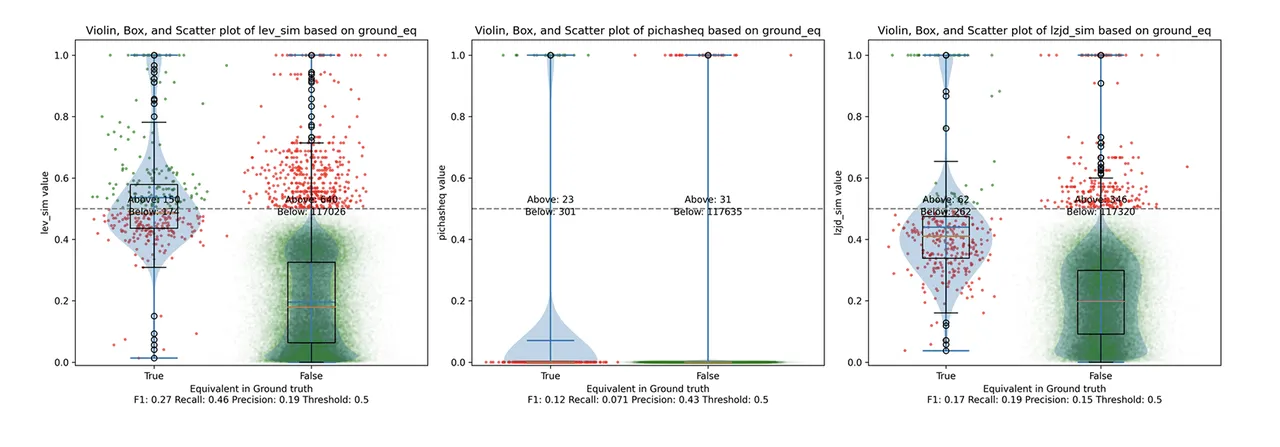
Determine 2: Violin Plot for “openssl gcc vs clang”. Click on to zoom in.
This visualization exhibits how properly every similarity metric differentiates the similarity distributions of equal and nonequivalent operate pairs. Clearly, the hallmark of similarity metric is that the distribution of equal capabilities needs to be increased than nonequivalent capabilities. Ideally, the similarity metric ought to produce distributions that don’t overlap in any respect, so we may draw a line between them. In apply, the distributions often intersect, and so as an alternative we’re pressured to make a tradeoff between precision and recall, as might be seen in Determine 1.
General, we are able to see from the violin plot that LEV and LZJD have a barely increased F1 rating (reported on the backside of the violin plot), however none of those strategies are doing a fantastic job. This suggests that gcc and clang produce code that’s fairly totally different syntactically.
Experiment 1b: openssl 1.1.1w Compiled With Completely different Optimization Ranges
The following comparability I did was to compile openssl 1.1.1w with gcc -g and optimization ranges -O0, -O1, -O2, -O3.
Evaluating Optimization Ranges -O0 and -O3
Let’s begin with one of many extremes, evaluating -O0 and -O3:
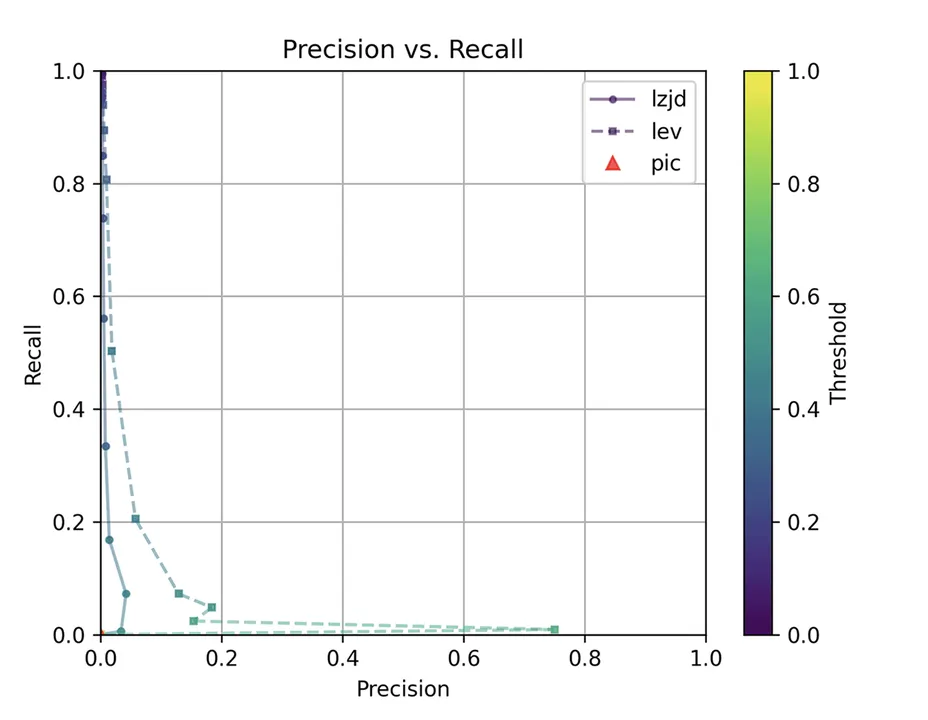
Determine 3: Precision vs. Recall Plot for “openssl -O0 vs -O3”
The very first thing you may be questioning about on this graph is, The place is PIC hashing? Properly, in the event you look intently, it is there at (0, 0). The violin plot provides us a bit extra details about what’s going on.
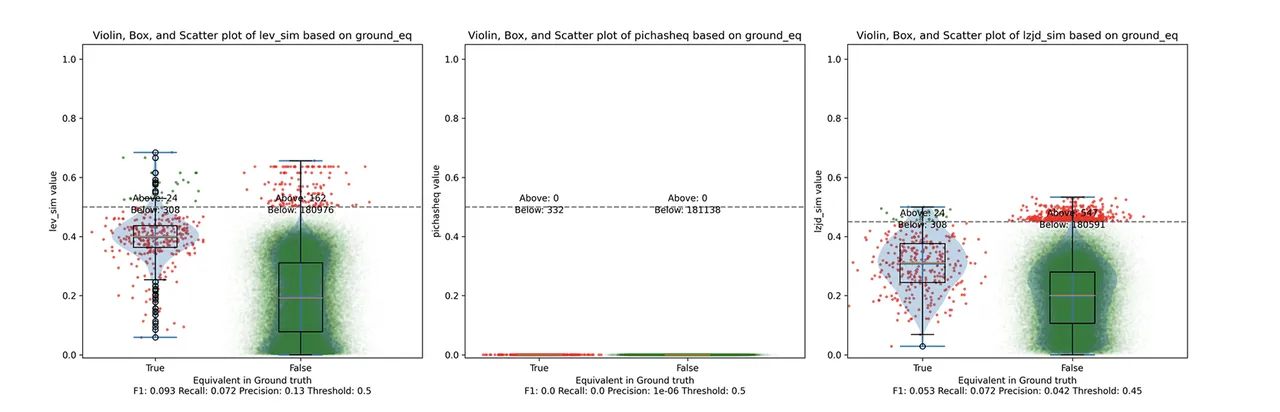
Determine 4: Violin Plot for “openssl -O0 vs -O3”. Click on to zoom in.
Right here we are able to see that PIC hashing made no constructive predictions. In different phrases, not one of the PIC hashes from the -O0 binary matched any of the PIC hashes from the -O3 binary. I included this experiment as a result of I assumed it might be very difficult for PIC hashing, and I used to be proper. However, after some dialogue with Cory, we realized one thing fishy was occurring. To attain a precision of 0.0, PIC hashing cannot discover any capabilities equal. That features trivially easy capabilities. In case your operate is only a ret there’s not a lot optimization to do.
Finally, I guessed that the -O0 binary didn’t use the -fomit-frame-pointer choice, whereas all different optimization ranges do. This issues as a result of this selection modifications the prologue and epilogue of each operate, which is why PIC hashing does so poorly right here.
LEV and LZJD do barely higher once more, attaining low (however nonzero) F1 scores. However to be truthful, not one of the strategies do very properly right here. It is a troublesome downside.
Evaluating Optimization Ranges -O2 and -O3
On the a lot simpler excessive, let’s take a look at -O2 and -O3.
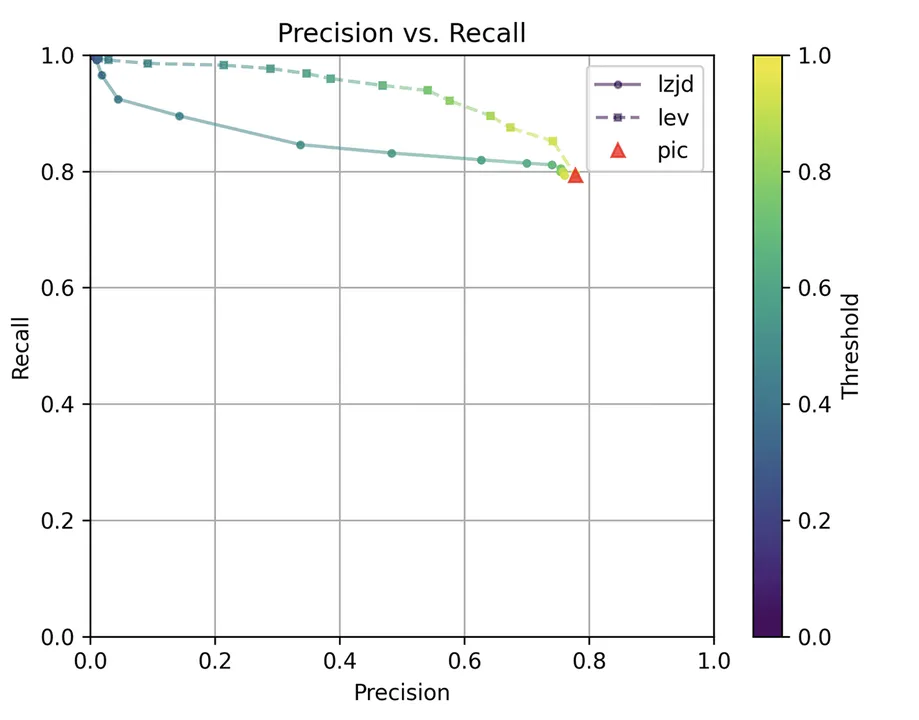
Determine 5: Precision vs. Recall Plot for “openssl -O2 vs -O3”
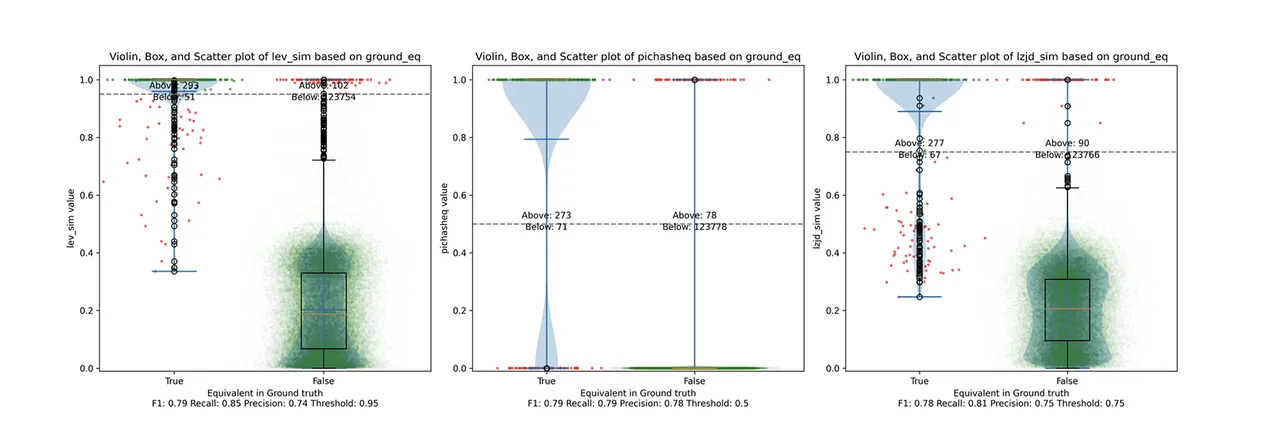
Determine 6: Violin Plot for “openssl -O1 vs -O2”. Click on to zoom in.
PIC hashing does fairly properly right here, attaining a recall of 0.79 and a precision of 0.78. LEV and LZJD do about the identical. Nevertheless, the precision vs. recall graph (Determine 11) for LEV exhibits a way more interesting tradeoff line. LZJD’s tradeoff line will not be almost as interesting, because it’s extra horizontal.
You can begin to see extra of a distinction between the distributions within the violin plots right here within the LEV and LZJD panels. I will name this one a three-way “tie.”
Evaluating Optimization Ranges -O1 and -O2
I might additionally anticipate -O1 and -O2 to be pretty related, however not as related as -O2 and -O3. Let’s examine:
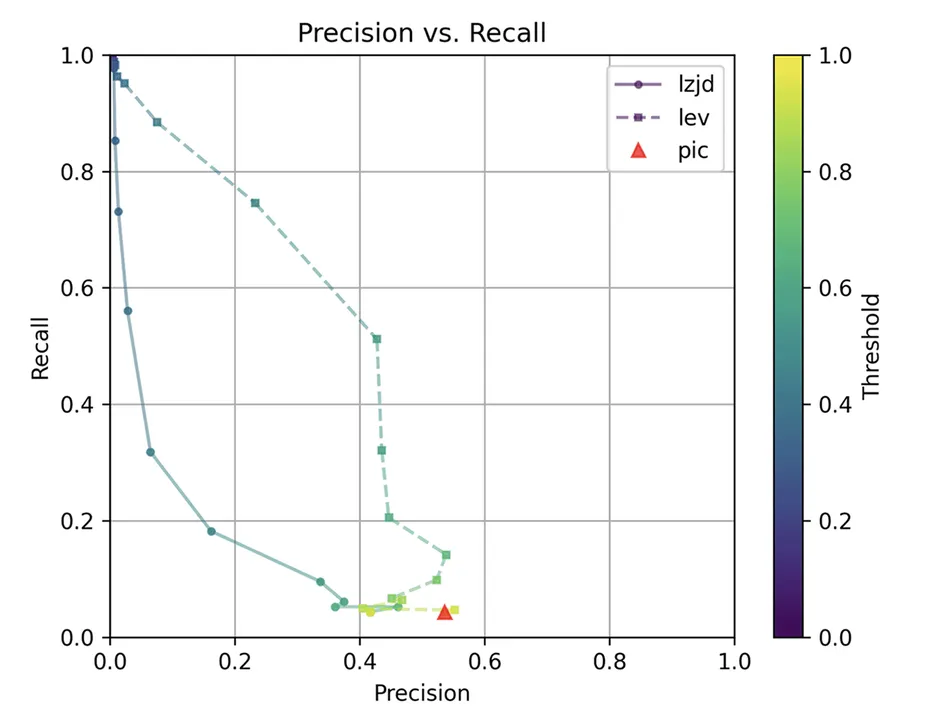
Determine 7: Precision vs. Recall Plot for “openssl -O1 vs -O2”
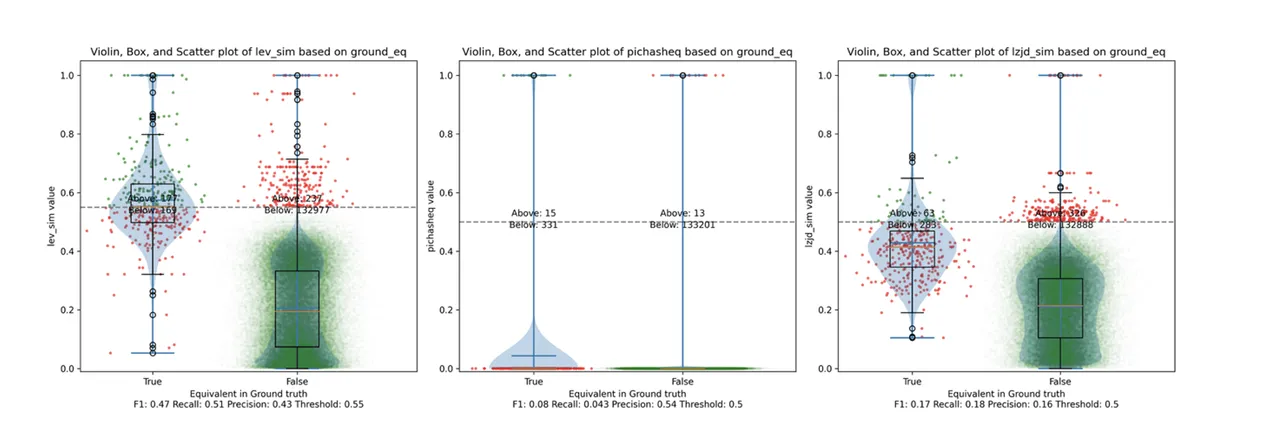
Determine 8: Violin Plot for “openssl -O1 vs -O2”. Click on to zoom in.
The precision vs. recall graph (Determine 7) is sort of fascinating. PIC hashing begins at a precision of 0.54 and a recall of 0.043. LEV shoots straight up, indicating that by decreasing the brink it’s potential to extend recall considerably with out shedding a lot precision. A very engaging tradeoff may be a precision of 0.43 and a recall of 0.51. That is the kind of tradeoff I hoped to see with fuzzy hashing.
Sadly, LZJD’s tradeoff line is once more not almost as interesting, because it curves within the unsuitable path.
We’ll say this can be a fairly clear win for LEV.
Evaluating Optimization Ranges -O1 and -O3
Lastly, let’s examine -O1 and -O3, that are totally different, however each have the -fomit-frame-pointer choice enabled by default.
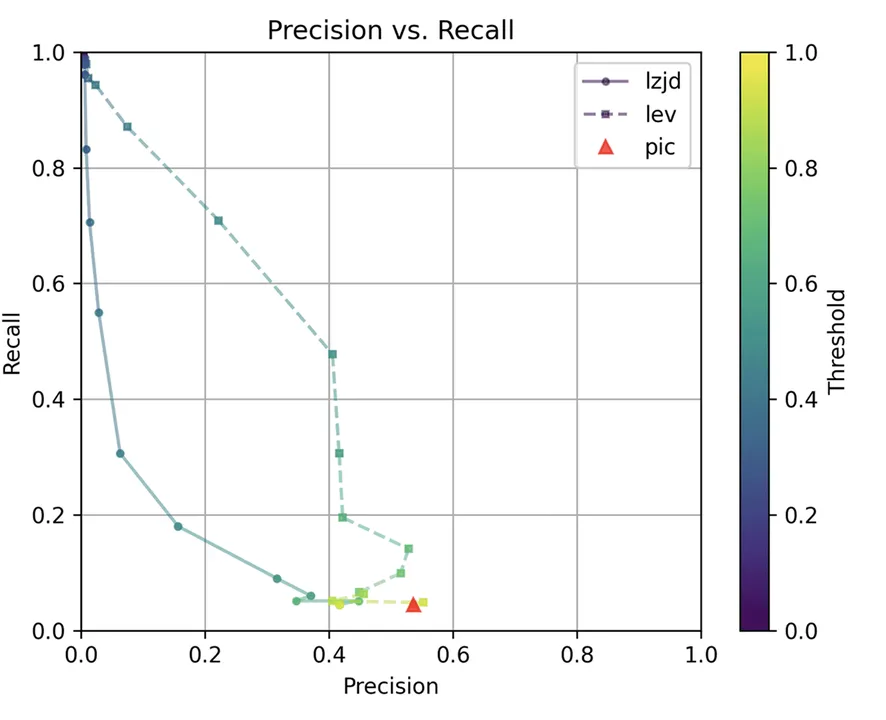
Determine 9: Precision vs. Recall Plot for “openssl -O1 vs -O3”
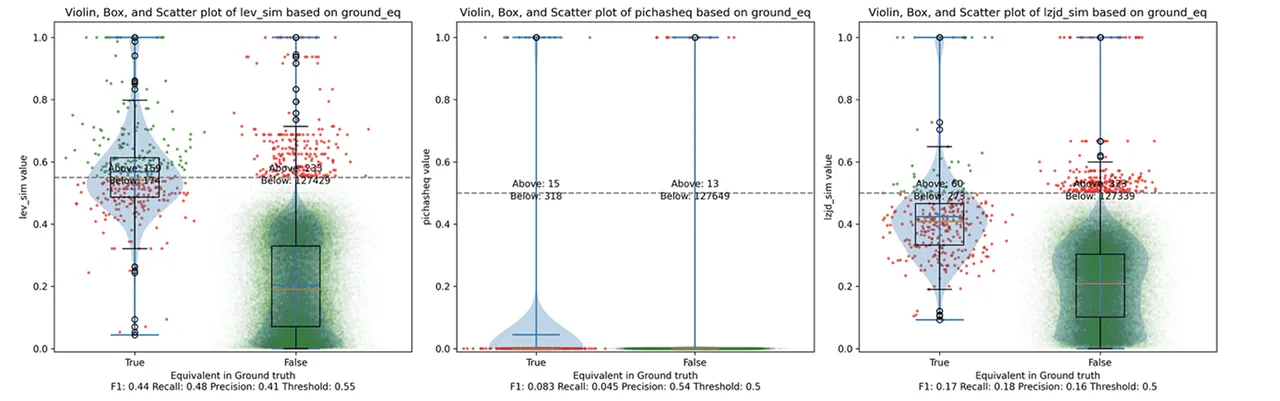
Determine 10: Violin Plot for “openssl -O1 vs -O3”. Click on to zoom in.
These graphs look virtually an identical to evaluating -O1 and -O2. I might describe the distinction between -O2 and -O3 as minor. So, it is once more a win for LEV.
Experiment 2: Completely different openssl Variations
The ultimate experiment I did was to match numerous variations of openssl. Cory urged this experiment as a result of he thought it was reflective of typical malware reverse engineering eventualities. The concept is that the malware creator launched Malware 1.0, which you reverse engineer. Later, the malware modifications just a few issues and releases Malware 1.1, and also you need to detect which capabilities didn’t change to be able to keep away from reverse engineering them once more.
I in contrast just a few totally different variations of openssl:
I compiled every model utilizing gcc -g -O2.
openssl 1.0 and 1.1 are totally different minor variations of openssl. As defined right here:
Letter releases, resembling 1.0.2a, solely include bug and safety fixes and no new options.
So, we’d anticipate that openssl 1.0.2u is pretty totally different from any 1.1.1 model. And, we’d anticipate that in the identical minor model, 1.1.1 could be just like 1.1.1q, however it might be extra totally different than 1.1.1w.
Experiment 2a: openssl 1.0.2u vs 1.1.1w
As earlier than, let’s begin with essentially the most excessive comparability: 1.0.2u vs 1.1.1w.
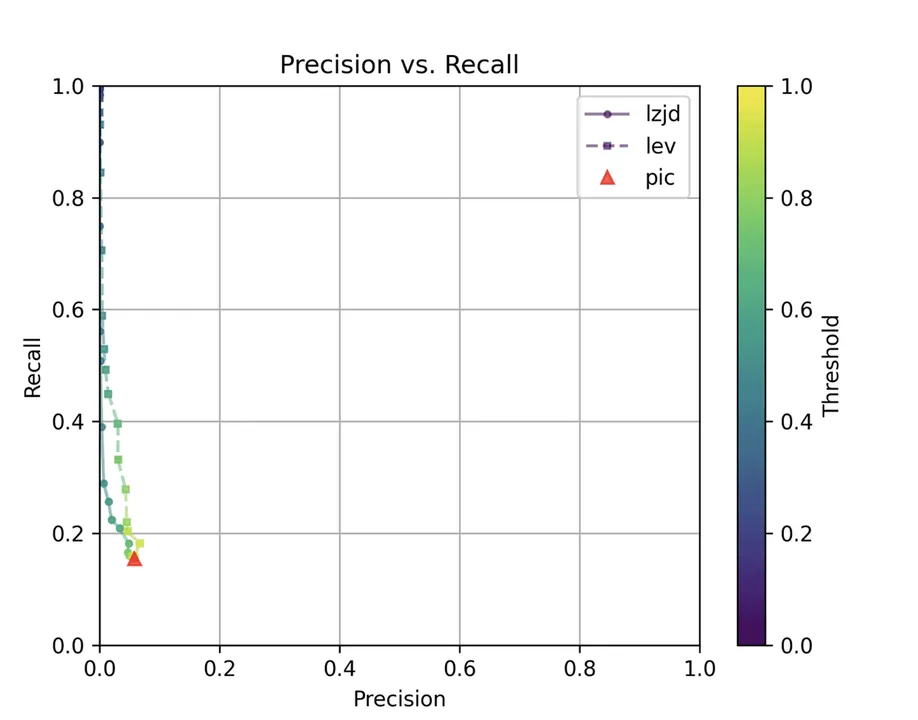
Determine 11: Precision vs. Recall Plot for “openssl 1.0.2u vs 1.1.1w”
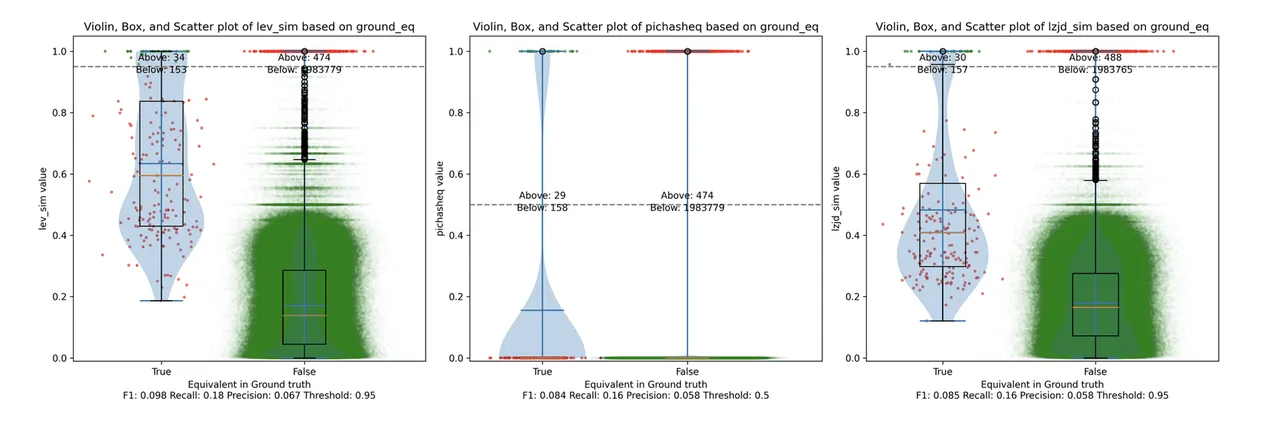
Determine 12: Violin Plot for “openssl 1.0.2u vs 1.1.1w”. Click on to zoom in.
Maybe not surprisingly, as a result of the 2 binaries are fairly totally different, all three strategies wrestle. We’ll say this can be a three means tie.
Experiment 2b: openssl 1.1.1 vs 1.1.1w
Now, let’s take a look at the unique 1.1.1 launch from September 2018 and examine it to the 1.1.1w bugfix launch from September 2023. Though numerous time has handed between the releases, the one variations needs to be bug and safety fixes.
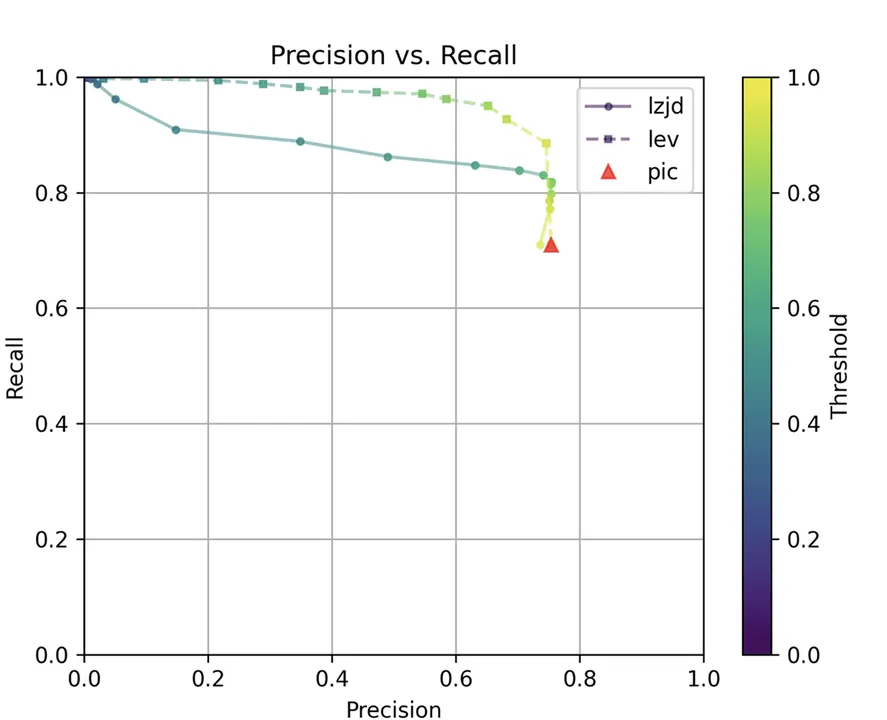
Determine 13: Precision vs. Recall Plot for “openssl 1.1.1 vs 1.1.1w”
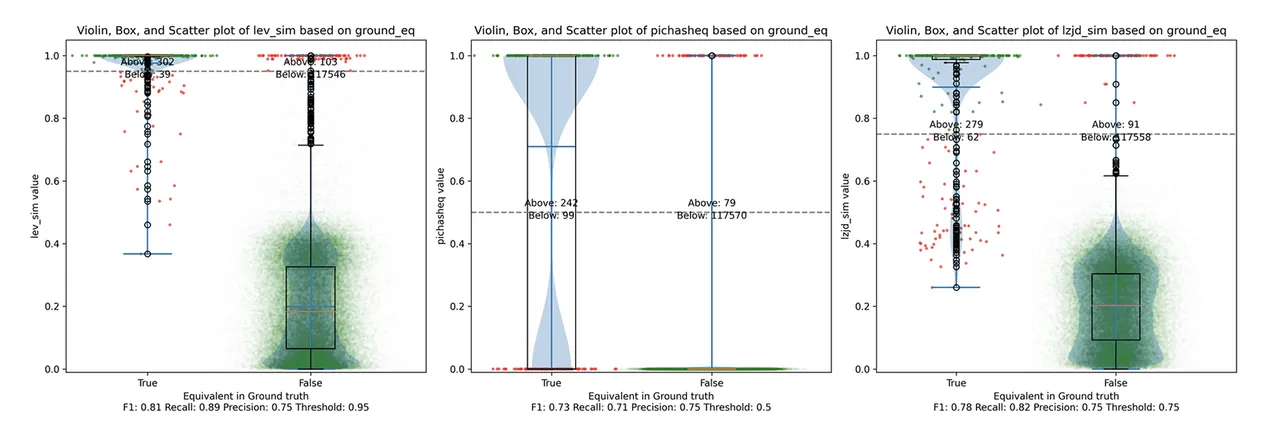
Determine 14: Violin Plot for “openssl 1.1.1 vs 1.1.1w”. Click on to zoom in.
All three strategies do a lot better on this experiment, presumably as a result of there are far fewer modifications. PIC hashing achieves a precision of 0.75 and a recall of 0.71. LEV and LZJD go virtually straight up, indicating an enchancment in recall with minimal tradeoff in precision. At roughly the identical precision (0.75), LZJD achieves a recall of 0.82 and LEV improves it to 0.89. LEV is the clear winner, with LZJD additionally displaying a transparent benefit over PIC.
Experiment 2c: openssl 1.1.1q vs 1.1.1w
Let’s proceed taking a look at extra related releases. Now we’ll examine 1.1.1q from July 2022 to 1.1.1w from September 2023.
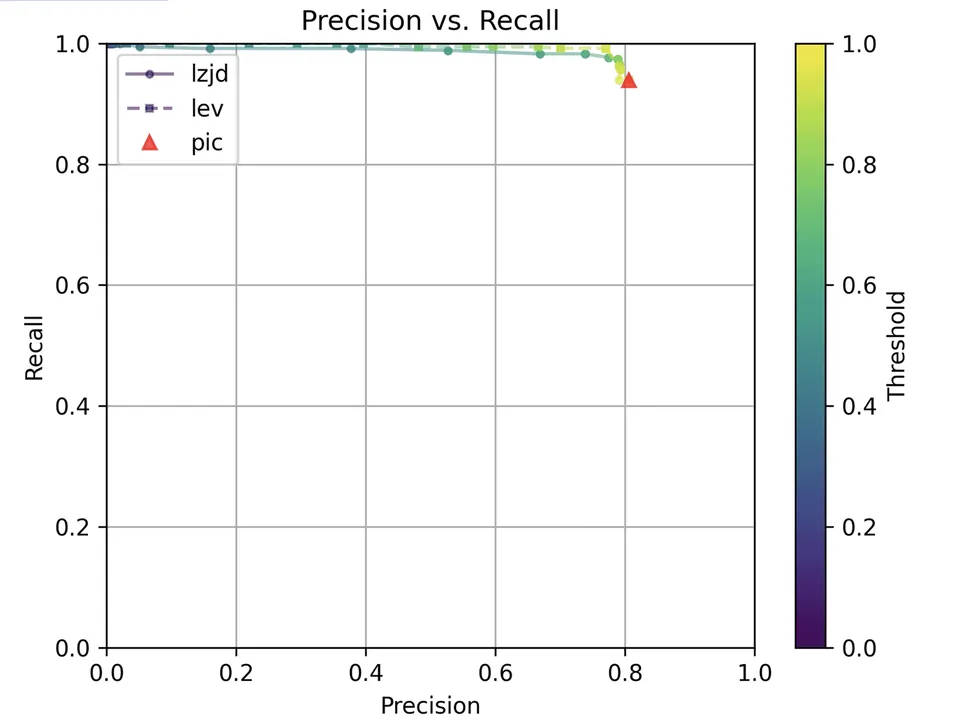
Determine 15: Precision vs. Recall Plot for “openssl 1.1.1q vs 1.1.1w”
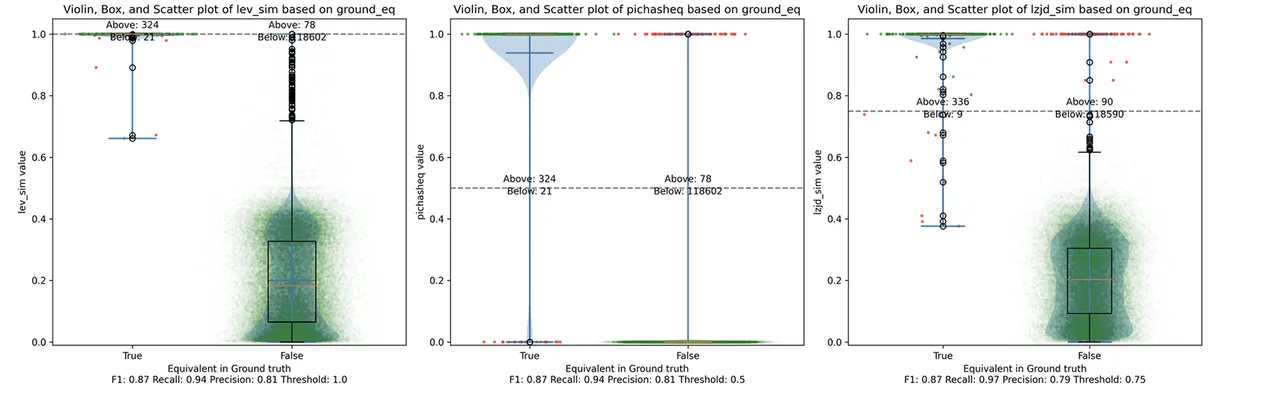
Determine 16: Violin Plot for “openssl 1.1.1q vs 1.1.1w”. Click on to zoom in.
As might be seen within the precision vs. recall graph (Determine 21), PIC hashing begins at a powerful precision of 0.81 and a recall of 0.94. There merely is not numerous room for LZJD or LEV to make an enchancment. This leads to a three-way tie.
Experiment second: openssl 1.1.1v vs 1.1.1w
Lastly, we’ll have a look at 1.1.1v and 1.1.1w, which have been launched solely a month aside.
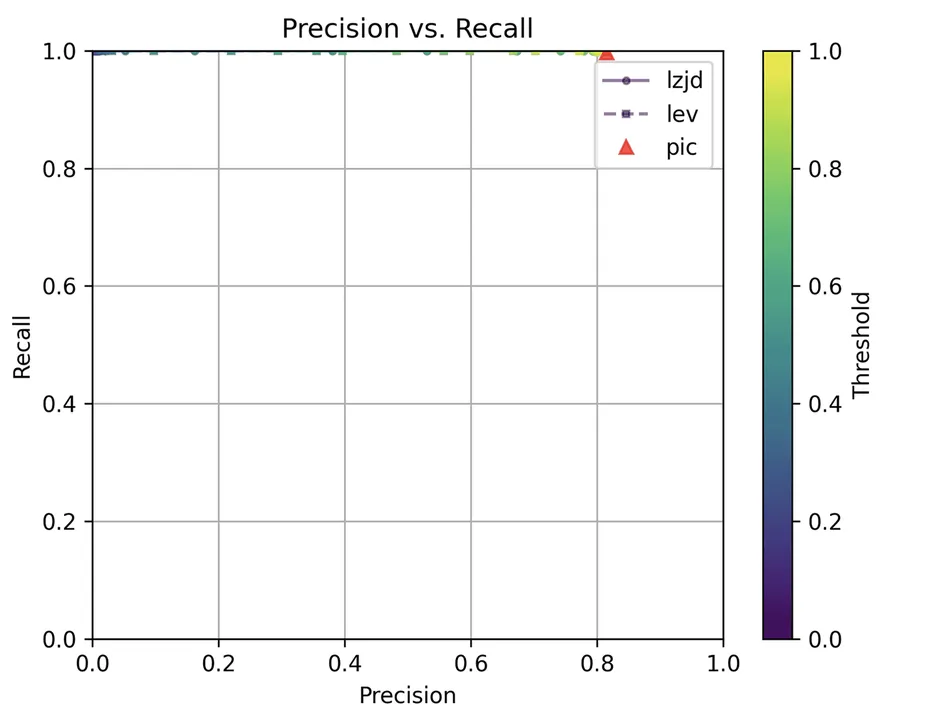
Determine 17: Precision vs. Recall Plot for “openssl 1.1.1v vs 1.1.1w”
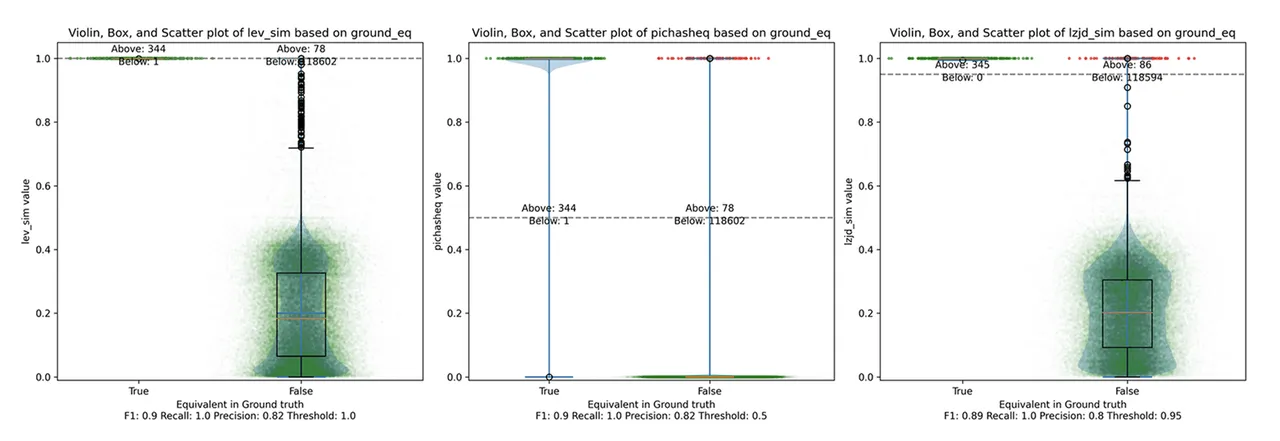
Determine 18: Violin Plot for “openssl 1.1.1v vs 1.1.1w”. Click on to zoom in.
Unsurprisingly, PIC hashing does even higher right here, with a precision of 0.82 and a recall of 1.0 (after rounding). Once more, there’s principally no room for LZJD or LEV to enhance. That is one other three means tie.
Conclusions: Thresholds in Follow
We noticed some eventualities by which LEV and LZJD outperformed PIC hashing. Nevertheless, it is essential to understand that we’re conducting these experiments with floor fact, and we’re utilizing the bottom fact to pick out the optimum threshold. You may see these thresholds listed on the backside of every violin plot. Sadly, in the event you look rigorously, you will additionally discover that the optimum thresholds will not be all the time the identical. For instance, the optimum threshold for LZJD within the “openssl 1.0.2u vs 1.1.1w” experiment was 0.95, but it surely was 0.75 within the “openssl 1.1.1q vs 1.1.1w” experiment.
In the true world, to make use of LZJD or LEV, it is advisable to choose a threshold. In contrast to in these experiments, you might not choose the optimum one, since you would don’t have any means of realizing in case your threshold was working properly or not. In case you select a poor threshold, you would possibly get considerably worse outcomes than PIC hashing.
PIC Hashing is Fairly Good
I feel we realized that PIC hashing is fairly good. It is not good, but it surely usually gives wonderful precision. In idea, LZJD and LEV can carry out higher by way of recall, which is interesting. In apply, nevertheless, it might not be clear that they’d as a result of you wouldn’t know which threshold to make use of. Additionally, though we did not discuss a lot about computational efficiency, PIC hashing may be very quick. Though LZJD is a lot quicker than LEV, it is nonetheless not almost as quick as PIC.
Think about you may have a database of 1,000,000 malware operate samples and you’ve got a operate that you just need to search for within the database. For PIC hashing, that is simply an ordinary database lookup, which might profit from indexing and different precomputation strategies. For fuzzy hash approaches, we would wish to invoke the similarity operate 1,000,000 instances every time we wished to do a database lookup.
There is a Restrict to Syntactic Similarity
Do not forget that we included LEV to symbolize the optimum similarity primarily based on the edit distance of instruction bytes. LEV didn’t considerably outperform PIC , which is sort of telling, and suggests that there’s a basic restrict to how properly syntactic similarity primarily based on instruction bytes can carry out. Surprisingly, PIC hashing seems to be near that restrict. We noticed a placing instance of this restrict when the body pointer was by accident omitted and, extra usually, all syntactic strategies wrestle when the variations turn out to be too nice.
It’s unclear whether or not any variants, like computing similarities over meeting code as an alternative of executable code bytes, would carry out any higher.
The place Do We Go From Right here?
There are in fact different methods for evaluating similarity, resembling incorporating semantic data. Many researchers have studied this. The overall draw back to semantic strategies is that they’re considerably costlier than syntactic strategies. However, in the event you’re keen to pay the upper computational worth, you may get higher outcomes.
Lately, a significant new function referred to as BSim was added to Ghidra. BSim can discover structurally related capabilities in probably giant collections of binaries or object information. BSim relies on Ghidra’s decompiler and may discover matches throughout compilers used, architectures, and/or small modifications to supply code.
One other fascinating query is whether or not we are able to use neural studying to assist compute similarity. For instance, we’d be capable to prepare a mannequin to grasp that omitting the body pointer doesn’t change the that means of a operate, and so should not be counted as a distinction.


