From the start, it has been thrilling to observe the rising variety of packages creating within the torch ecosystem. What’s superb is the number of issues folks do with torch: prolong its performance; combine and put to domain-specific use its low-level computerized differentiation infrastructure; port neural community architectures … and final however not least, reply scientific questions.
This weblog submit will introduce, in brief and relatively subjective type, one in every of these packages: torchopt. Earlier than we begin, one factor we must always most likely say much more usually: Should you’d prefer to publish a submit on this weblog, on the package deal you’re creating or the best way you use R-language deep studying frameworks, tell us – you’re greater than welcome!
torchopt
torchopt is a package deal developed by Gilberto Camara and colleagues at Nationwide Institute for House Analysis, Brazil.
By the look of it, the package deal’s cause of being is relatively self-evident. torch itself doesn’t – nor ought to it – implement all of the newly-published, potentially-useful-for-your-purposes optimization algorithms on the market. The algorithms assembled right here, then, are most likely precisely these the authors had been most desperate to experiment with in their very own work. As of this writing, they comprise, amongst others, varied members of the favored ADA* and *ADAM* households. And we might safely assume the checklist will develop over time.
I’m going to introduce the package deal by highlighting one thing that technically, is “merely” a utility operate, however to the consumer, might be extraordinarily useful: the flexibility to, for an arbitrary optimizer and an arbitrary take a look at operate, plot the steps taken in optimization.
Whereas it’s true that I’ve no intent of evaluating (not to mention analyzing) completely different methods, there’s one which, to me, stands out within the checklist: ADAHESSIAN (Yao et al. 2020), a second-order algorithm designed to scale to massive neural networks. I’m particularly curious to see the way it behaves as in comparison with L-BFGS, the second-order “traditional” accessible from base torch we’ve had a devoted weblog submit about final 12 months.
The way in which it really works
The utility operate in query is called test_optim(). The one required argument considerations the optimizer to attempt (optim). However you’ll possible need to tweak three others as effectively:
test_fn: To make use of a take a look at operate completely different from the default (beale). You’ll be able to select among the many many supplied intorchopt, or you’ll be able to go in your individual. Within the latter case, you additionally want to supply details about search area and beginning factors. (We’ll see that instantly.)steps: To set the variety of optimization steps.opt_hparams: To switch optimizer hyperparameters; most notably, the training charge.
Right here, I’m going to make use of the flower() operate that already prominently figured within the aforementioned submit on L-BFGS. It approaches its minimal because it will get nearer and nearer to (0,0) (however is undefined on the origin itself).
Right here it’s:
flower <- operate(x, y) {
a <- 1
b <- 1
c <- 4
a * torch_sqrt(torch_square(x) + torch_square(y)) + b * torch_sin(c * torch_atan2(y, x))
}To see the way it appears to be like, simply scroll down a bit. The plot could also be tweaked in a myriad of how, however I’ll stick to the default structure, with colours of shorter wavelength mapped to decrease operate values.
Let’s begin our explorations.
Why do they all the time say studying charge issues?
True, it’s a rhetorical query. However nonetheless, generally visualizations make for probably the most memorable proof.
Right here, we use a preferred first-order optimizer, AdamW (Loshchilov and Hutter 2017). We name it with its default studying charge, 0.01, and let the search run for two-hundred steps. As in that earlier submit, we begin from distant – the purpose (20,20), manner exterior the oblong area of curiosity.
library(torchopt)
library(torch)
test_optim(
# name with default studying charge (0.01)
optim = optim_adamw,
# go in self-defined take a look at operate, plus a closure indicating beginning factors and search area
test_fn = checklist(flower, operate() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
steps = 200
)
Whoops, what occurred? Is there an error within the plotting code? – Under no circumstances; it’s simply that after the utmost variety of steps allowed, we haven’t but entered the area of curiosity.
Subsequent, we scale up the training charge by an element of ten.

What a change! With ten-fold studying charge, the result’s optimum. Does this imply the default setting is unhealthy? In fact not; the algorithm has been tuned to work effectively with neural networks, not some operate that has been purposefully designed to current a selected problem.
Naturally, we additionally should see what occurs for but larger a studying charge.

We see the habits we’ve all the time been warned about: Optimization hops round wildly, earlier than seemingly heading off ceaselessly. (Seemingly, as a result of on this case, this isn’t what occurs. As an alternative, the search will bounce distant, and again once more, repeatedly.)
Now, this would possibly make one curious. What really occurs if we select the “good” studying charge, however don’t cease optimizing at two-hundred steps? Right here, we attempt three-hundred as an alternative:

Curiously, we see the identical type of to-and-fro taking place right here as with a better studying charge – it’s simply delayed in time.
One other playful query that involves thoughts is: Can we observe how the optimization course of “explores” the 4 petals? With some fast experimentation, I arrived at this:

Who says you want chaos to supply a phenomenal plot?
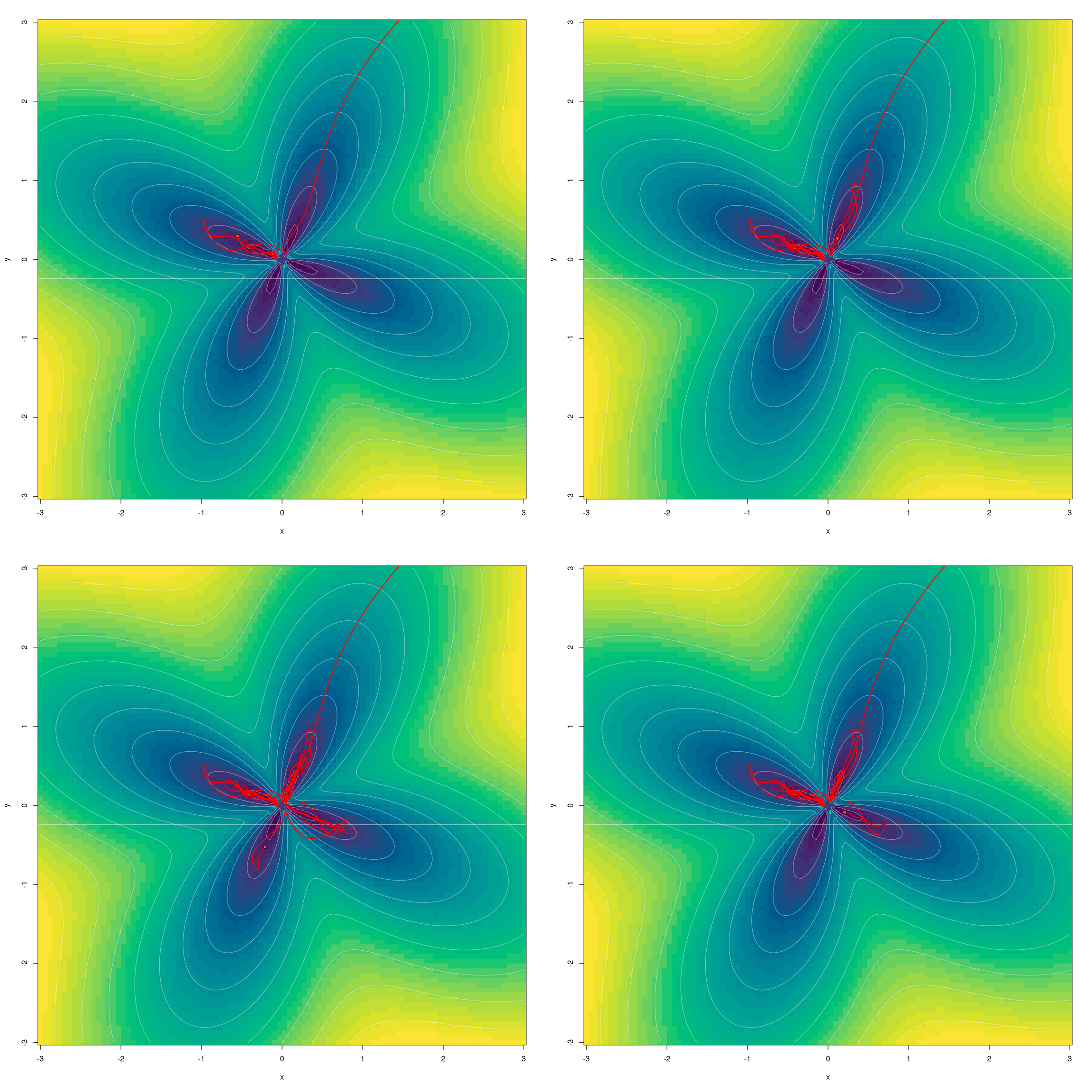
A second-order optimizer for neural networks: ADAHESSIAN
On to the one algorithm I’d like to take a look at particularly. Subsequent to just a little little bit of learning-rate experimentation, I used to be capable of arrive at a superb outcome after simply thirty-five steps.

Given our current experiences with AdamW although – that means, its “simply not settling in” very near the minimal – we might need to run an equal take a look at with ADAHESSIAN, as effectively. What occurs if we go on optimizing fairly a bit longer – for two-hundred steps, say?

Like AdamW, ADAHESSIAN goes on to “discover” the petals, however it doesn’t stray as distant from the minimal.
Is that this stunning? I wouldn’t say it’s. The argument is similar as with AdamW, above: Its algorithm has been tuned to carry out effectively on massive neural networks, to not clear up a traditional, hand-crafted minimization activity.
Now we’ve heard that argument twice already, it’s time to confirm the specific assumption: {that a} traditional second-order algorithm handles this higher. In different phrases, it’s time to revisit L-BFGS.
Better of the classics: Revisiting L-BFGS
To make use of test_optim() with L-BFGS, we have to take just a little detour. Should you’ve learn the submit on L-BFGS, you might keep in mind that with this optimizer, it’s essential to wrap each the decision to the take a look at operate and the analysis of the gradient in a closure. (The reason is that each should be callable a number of instances per iteration.)
Now, seeing how L-BFGS is a really particular case, and few persons are possible to make use of test_optim() with it sooner or later, it wouldn’t appear worthwhile to make that operate deal with completely different circumstances. For this on-off take a look at, I merely copied and modified the code as required. The outcome, test_optim_lbfgs(), is discovered within the appendix.
In deciding what variety of steps to attempt, we take note of that L-BFGS has a distinct idea of iterations than different optimizers; that means, it might refine its search a number of instances per step. Certainly, from the earlier submit I occur to know that three iterations are adequate:

At this level, in fact, I want to stay with my rule of testing what occurs with “too many steps.” (Though this time, I’ve robust causes to imagine that nothing will occur.)

Speculation confirmed.
And right here ends my playful and subjective introduction to torchopt. I definitely hope you preferred it; however in any case, I believe you need to have gotten the impression that here’s a helpful, extensible and likely-to-grow package deal, to be watched out for sooner or later. As all the time, thanks for studying!
Appendix
test_optim_lbfgs <- operate(optim, ...,
opt_hparams = NULL,
test_fn = "beale",
steps = 200,
pt_start_color = "#5050FF7F",
pt_end_color = "#FF5050FF",
ln_color = "#FF0000FF",
ln_weight = 2,
bg_xy_breaks = 100,
bg_z_breaks = 32,
bg_palette = "viridis",
ct_levels = 10,
ct_labels = FALSE,
ct_color = "#FFFFFF7F",
plot_each_step = FALSE) {
if (is.character(test_fn)) {
# get beginning factors
domain_fn <- get(paste0("domain_",test_fn),
envir = asNamespace("torchopt"),
inherits = FALSE)
# get gradient operate
test_fn <- get(test_fn,
envir = asNamespace("torchopt"),
inherits = FALSE)
} else if (is.checklist(test_fn)) {
domain_fn <- test_fn[[2]]
test_fn <- test_fn[[1]]
}
# start line
dom <- domain_fn()
x0 <- dom[["x0"]]
y0 <- dom[["y0"]]
# create tensor
x <- torch::torch_tensor(x0, requires_grad = TRUE)
y <- torch::torch_tensor(y0, requires_grad = TRUE)
# instantiate optimizer
optim <- do.name(optim, c(checklist(params = checklist(x, y)), opt_hparams))
# with L-BFGS, it's essential to wrap each operate name and gradient analysis in a closure,
# for them to be callable a number of instances per iteration.
calc_loss <- operate() {
optim$zero_grad()
z <- test_fn(x, y)
z$backward()
z
}
# run optimizer
x_steps <- numeric(steps)
y_steps <- numeric(steps)
for (i in seq_len(steps)) {
x_steps[i] <- as.numeric(x)
y_steps[i] <- as.numeric(y)
optim$step(calc_loss)
}
# put together plot
# get xy limits
xmax <- dom[["xmax"]]
xmin <- dom[["xmin"]]
ymax <- dom[["ymax"]]
ymin <- dom[["ymin"]]
# put together information for gradient plot
x <- seq(xmin, xmax, size.out = bg_xy_breaks)
y <- seq(xmin, xmax, size.out = bg_xy_breaks)
z <- outer(X = x, Y = y, FUN = operate(x, y) as.numeric(test_fn(x, y)))
plot_from_step <- steps
if (plot_each_step) {
plot_from_step <- 1
}
for (step in seq(plot_from_step, steps, 1)) {
# plot background
picture(
x = x,
y = y,
z = z,
col = hcl.colours(
n = bg_z_breaks,
palette = bg_palette
),
...
)
# plot contour
if (ct_levels > 0) {
contour(
x = x,
y = y,
z = z,
nlevels = ct_levels,
drawlabels = ct_labels,
col = ct_color,
add = TRUE
)
}
# plot start line
factors(
x_steps[1],
y_steps[1],
pch = 21,
bg = pt_start_color
)
# plot path line
traces(
x_steps[seq_len(step)],
y_steps[seq_len(step)],
lwd = ln_weight,
col = ln_color
)
# plot finish level
factors(
x_steps[step],
y_steps[step],
pch = 21,
bg = pt_end_color
)
}
}