What’s Correlation?
A statistical device that helps within the research of the connection between two variables is named Correlation. It additionally helps in understanding the financial behaviour of the variables. Nevertheless, correlation doesn’t inform something in regards to the cause-and-effect relationship between the 2 variables. Correlation might be measured via three completely different strategies; viz., Scatter Diagram, Karl Pearson’s Coefficient of Correlation, and Spearman’s Rank Correlation Coefficient.
In accordance with L.R. Connor, “If two or extra portions fluctuate in sympathy in order that actions in a single are usually accompanied by corresponding actions in others, then they’re mentioned to be correlated.”
What’s a Scatter Diagram?
A easy and engaging technique of measuring correlation by diagrammatically representing bivariate distribution for willpower of the character of the correlation between the variables is named Scatter Diagram Technique. This technique provides a visible thought to the investigator/analyst relating to the character of the affiliation between the 2 variables. It’s the easiest technique of finding out the connection between two variables as there is no such thing as a must calculate any numerical worth.
How to attract a Scatter Diagram?
The 2 steps required to attract a Scatter Diagram or Dot Diagram are as follows:
- Plot the values of the given variables (say X and Y) alongside the X-axis and Y-axis, respectively.
- Present these plotted values on the graph by dots. Every of those dots represents a pair of values.
Interpretation of Scatter Diagram
After observing the sample of dots, one can know the presence or absence of correlation and its kind. Moreover, it additionally provides an thought of the character and depth of the connection between the 2 variables.
The scatter diagram might be interpreted within the following methods:
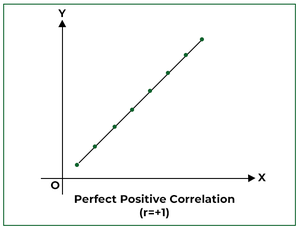
1. Good Optimistic Correlation:
If the factors of the scatter diagram fall on a straight line and have a constructive(upward) slope, then the correlation is alleged to be completely constructive; i.e., r = +1.
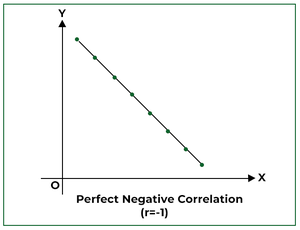
2. Good Adverse Correlation:
If the factors of the scatter diagram fall on a straight line and have a detrimental(downward) slope, then the correlation is alleged to be completely detrimental; i.e., r = -1.
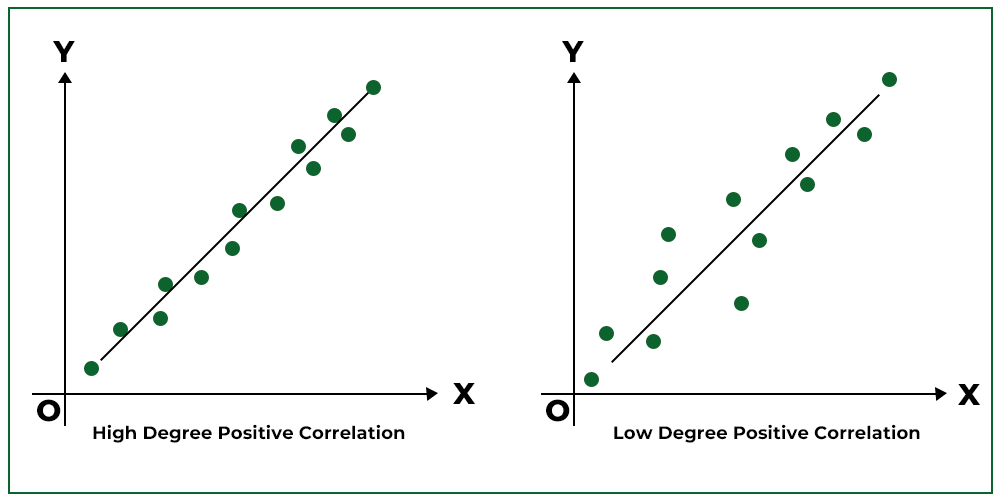
3. Optimistic Correlation:
When the factors of the scatter diagram cluster round a straight line (upward slope from left to proper), then the correlation is alleged to be constructive.
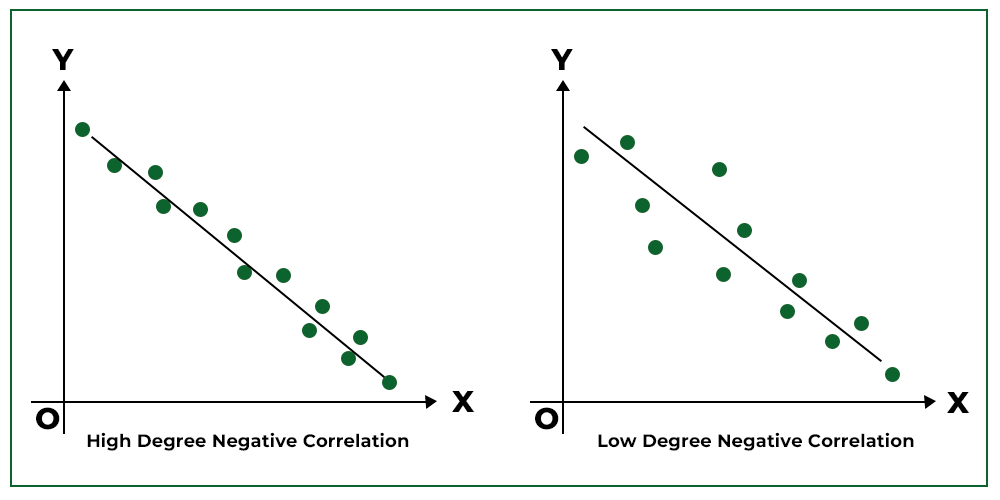
4. Adverse Correlation:
When the factors of the scatter diagram cluster round a straight line (downward/detrimental slope), then the correlation is alleged to be detrimental.
5. No Correlation:
When the factors of the scatter diagram are scattered in a haphazard method, then there’s zero or no correlation.
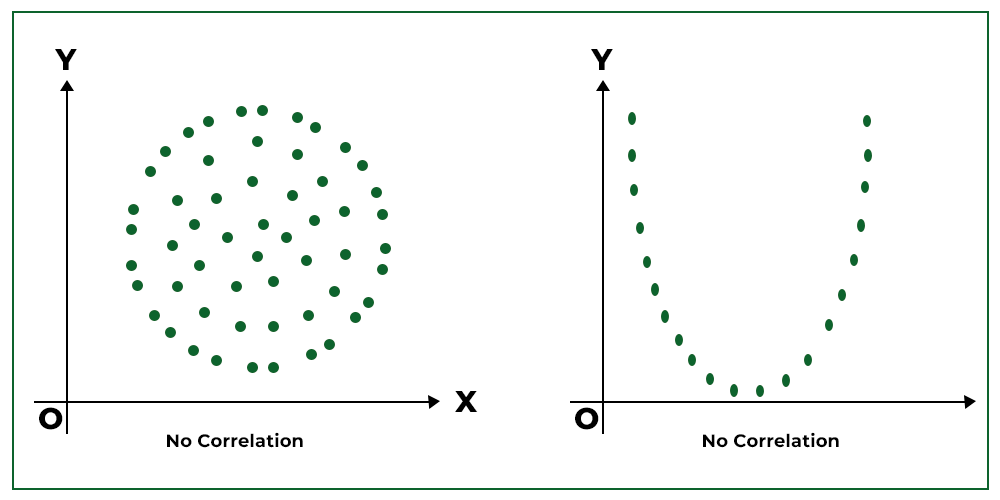
Learn how to interpret a Scatter Diagram?
Whereas deciphering a scatter diagram, the given beneath factors ought to be considered:
- Dense or Scattered Factors: If the plotted factors are shut to one another, then the analyst can anticipate a excessive diploma of correlation between the 2 variables. Nevertheless, if the plotted factors are extensively scattered, then the analyst can anticipate a poor correlation between the variables.
- Pattern or No Pattern: If the factors plotted on the scatter diagram reveals any development both upward or downward, then it may be mentioned that the variables are correlated. Nevertheless, if the plotted factors don’t present any development, then it may be mentioned that the variables are uncorrelated.
- Upward or Downward Pattern: If the plotted factors present an upward development rising from the decrease left-hand nook of the graph and goes upward to the higher right-hand nook, then the correlation is constructive. It implies that the 2 variables transfer in the identical route. Nevertheless, if the plotted factors present a downward development from the higher left-hand nook of the graph to the decrease right-hand nook, then the correlation is detrimental. It implies that the 2 variables transfer in the other way.
- Good Correlation: If the factors plotted on the scatter diagram lie on a straight line and have a constructive slope, then it may be mentioned that the correlation is ideal and constructive. Nevertheless, if the factors plotted lie on a straight line and have a detrimental slope, then it may be mentioned that the correlation is ideal and detrimental.
Instance:
Draw a Scatter Diagram for the next knowledge and state the kind of correlation between the given two variables X and Y.

Resolution:
We’ll draw the scatter diagram by plotting the values of Collection X on the X-axis and values of Collection y on the Y-axis (10, 80), (20, 160),………(60, 480).
.png)
We are able to see that every one the factors of the given two variables X and Y are plotted on a positively sloping straight line, which implies that there’s a Optimistic Correlation between the values of Collection X and Y.
Deserves of Scatter Diagram
1. Simplicity: Scatter Diagram is an easy and non-mathematical technique to check correlation between two variables.
2. First Step: It is step one of investigating the connection between two variables.
3. Simply Comprehensible: One can simply perceive and interpret scatter diagrams. Moreover, solely at a single look on the diagram, one can simply inform the presence or absence of correlation.
4. Not Affected by Excessive Objects: The scale of maximum values doesn’t have an effect on the scatter diagram. It’s a high quality which isn’t current in most mathematical strategies.
Demerits of Scatter Diagram
1. Tough Measure: Scatter diagram solely provides a tough thought of the diploma and nature of correlation between the given two variables. Subsequently, it’s only a qualitative expression relatively than a quantitative expression.
2. Non-mathematical Technique: Like different strategies of correlation, Scatter Diagram Technique doesn’t point out the precise numerical worth of correlation.
3. Unsuitable for Giant Observations: If there are greater than two variables, it turns into tough to attract a scatter diagram.


